Курсовая работа: Однородные и неоднородные системы линейных дифференциальных уравнений
(j = 1, 2, …,n), (18)
Коэффициенты α j ( 1 ) и α j (2) определяются из системы уравнений (13).
Можно показать, что действительные и мнимые части комплексного решения тоже являются решениями. Таким образом, мы получаем два частных решения:
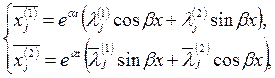(19)
Где 
- действительные числа, определяемые через 
и 
. Соответствующие комбинации функций (18) войдут в общее решение системы. [2 стр 112-115]
Случай 3. Характеристическое уравнение имеет единственный корень k (кратности 2), которому соответствуют два линейно независимых собственных вектора P1 и P2 (т.е. кратность корня совпадает с числом линейно независимых собственных векторов). Векторы P1 и P2 порождают два линейно независимых решения
И общее решение, так же как и в случае 1, находится по формуле (4) .
Случай 4. Характеристическое уравнение имеет единственный корень k (кратности 2), которому с точностью до постоянного множителя соответствует один собственный вектор P1 (т.е. кратность корня больше числа линейно независимых собственных векторов). В этом случае для отыскания решения целесообразно применить метод неопределенных коэффициентов . Согласно этому методу общее решение необходимо искать в форме
Где постоянные Сij требуют определения путем подстановки этих выражений в исходную однородную систему.
Замечание. Для решения однородных систем в случае, когда корень характеристического уравнения λ кратный и ему соответствует единственный собственный вектор P1 , может быть применен метод присоединения векторов .
Суть его такова. Пусть P2 – вектор-столбец, являющийся решением уравнения
(20)
тогда однородная система
(21)
имеет два линейно независимых решения
.
Покажем, что Y2 является решением. Имеем
.
Учитывая, что P1 и - собственный вектор, а P2 удовлетворяет условию (20), получаем
.
Нетрудно также убедиться, что Y1 и Y2 линейно независимы. Следовательно, они образуют фундаментальный набор решений, и общее решение может быть найдено по формуле (4).
В общем случае корню характеристического уравнения λ кратности k>1, имеющему один собственный вектор P1 ,соответствует k линейно независимых решений
, (22)
Где присоединенные векторы P2 ,P3 ,…,Pk являются последовательными решениями следующих алгебраических систем
(23) [3 стр 519-522]