Курсовая работа: Однородные и неоднородные системы линейных дифференциальных уравнений

X₁ =α₁ e^kt , X₂ =α₂ e^kt ,……. X_n =α_n e^kt . (12)

Требуется определить постоянные α_1, α₂ ,…, α_n и k так, чтобы функции α₁ e^kt , α₂ e^kt ,…,α_n e^kt удовлетворяли системе уравнений (11). Подставим их в систему(1), получим:

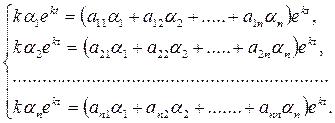
Сократим на e^kt . Перенося все члены в одну сторону и собирая коэффициенты при α_1, α₂ ,…., α_n , получим систему уравнений

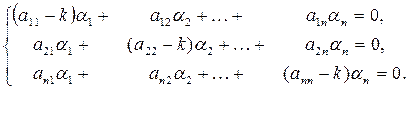
Выберем α_1, α₂ ,…., α_n и k такими, чтобы удовлетворялась система (13).Эта система есть система линейных однородных алгебраических уравнений относительно α_1, α₂ ,…., α_n . Составим определитель системы (13):

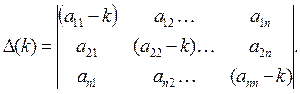(14)

Если k таково, что определитель ∆ отличен от нуля, то система (13) имеет только нулевые решения α₁ =α₂ =…=α_n =0,а следовательно, формулы (12) дают только тривиальные решения:

X₁ (t)=X₂ (t)=…=X(t)=0.

Таким образом, нетривиальные решения (12) мы получим только при таких k,при которых определитель (14) обращается в нуль. Мы приходим к уравнению n-ого порядка для определения k:

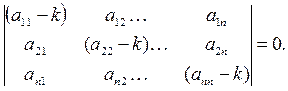(15)

Это уравнение называется характеристическим уравнением для системы (1),его корни называются корнями характеристического уравнения.

Рассмотрим несколько случаев.

Случай 1. Корни характеристического уравнения действительны и различны. Обозначим через k₁ , k₂ ,….k_n корни характеристического уравнения. Для каждого корня k_j напишем систему (13) и определим коэффициенты

α₁ ^{( i )} ,α₂ ^{( i )} ,…, α_n ^{( i )} .

Можно показать, что один из них произвольный, его можно считать равным единице. Таким образом, получаем:

для корня k₁ решение системы (11)

Для корня k₂ решение системы (1)

……………………………………………………….

для корней k_n решение системы (1)

Путем непосредственной подстановки в уравнения можно убедиться, что система функций

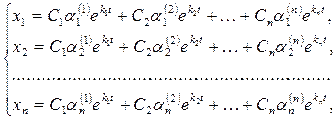(16)

где С₁ , С₂ ,….,С_n -произвольные постоянные, тоже является решением системы дифференциальных уравнений (11). Это есть общее решение системы (11). Легко показать, что можно найти такие значения постоянных, при которых решение будет удовлетворять заданным начальным условиям.

Случай 2. Корни характеристического уравнения различные, но среди них есть комплексные. Пусть среди корней характеристического уравнения имеется два комплексных сопряженных корня:

k₁ = α+iβ, k₂ = α-iβ.

Этим корням будут соответствовать решения