Курсовая работа: Однородные и неоднородные системы линейных дифференциальных уравнений

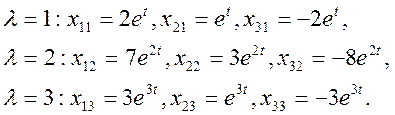
Общее решение записываем в виде

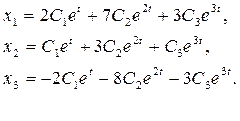
Случай 2.

Пример 1.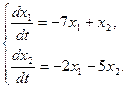

Решение. Составляем характеристическое уравнение

или

и находим его корни:

Подставляем в систему (3) и определяем и :

или

Откуда . Полагая , получаем .

Пишем решение (7):

Подставляя в систему (3), находим:

.

Получим вторую систему решений (8):

Перепишем решения:

или

За системы частных решений можно взять отдельно действительные части и отдельно мнимые части

Общим решением системы будет

Пример 2.

Решение. Составляем характеристическое уравнение

или