Курсовая работа: Однородные и неоднородные системы линейных дифференциальных уравнений
Таким образом, мы получили решение системы:
![]()
![]()
Составим далее систему (3) для корня ![]() и определяем
и определяем ![]() и
и ![]() :
:
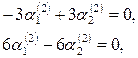
Откуда ![]() и
и ![]() =1,
=1, ![]() =1.
=1.
Получаем второе решение системы:
![]()
![]()
Общее решение системы будет
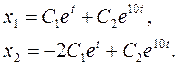
Пример3. 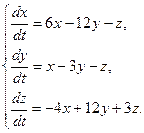
Решение. Составим характеристическое уравнение матрицы системы
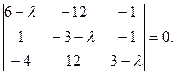
Раскрывая определитель, находим
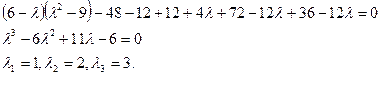
Составим систему (3) для корня ![]()
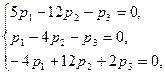
одно из которых - следствие двух других. Возьмем, например, первые два уравнения:
![]()
![]()
Отсюда
![]()
![]()
![]()
Приняв k=1/4,получаем собственный вектор (2;1;-2).
При λ=2 имеет систему
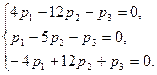
Используя первые два уравнения (третье – их следствие), находим
![]()
![]()
![]()
Полагая k=1, находим собственный вектор (7;3;-8).
При λ=3 имеет систему
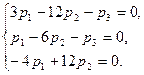
Из последнего уравнения находим ![]() Подставляем это значение p1 в первое уравнение и находим
Подставляем это значение p1 в первое уравнение и находим ![]() Приняв
Приняв ![]() получаем
получаем ![]()
![]() т.е. собственный вектор (3; 1; -3).
т.е. собственный вектор (3; 1; -3).