Курсовая работа: Опис та типологія коливань
Це вираження може бути написане також і у вигляді
![]() (1,8)
(1,8)
Оскільки cos (ωt + α) = cos ωt cos α — sin ωt sin α, те порівняння з (1,7) показує, що довільні постійні ![]() пов'язані з постійними
пов'язані з постійними ![]() співвідношеннями
співвідношеннями
![]() (1.9)
(1.9)
Таким чином, поблизу положення стійкої рівноваги система робить гармонійний коливальний рух. Коефіцієнт а при періодичному множнику в (1,8) називається амплітудою коливань, а аргумент косинуса — їхньою фазою ; а є початкове значення фази, що залежить, мабуть, від вибору початку відліку часу. Величина ω називається циклічною частотою коливань; у теоретичній фізиці, втім, її називають звичайно просто частотою , що ми й будемо робити надалі.
Частота є основною характеристикою коливань, що не залежить від початкових умов руху. Відповідно до формули (1,6) вона цілком визначається властивостями механічної системи як такої. Підкреслимо, однак, що ця властивість частоти пов'язане з передбачуваною малістю коливань і зникає при переході до більше високих наближень. З математичної точки зору воно пов'язане із квадратичною залежністю потенційної енергії від координати.
Енергія системи, що робить малі коливання, є
![]()
або, підставивши сюди (21,8):
![]() (1,10)
(1,10)
Вона пропорційна квадрату амплітуди коливань.
Залежність координати коливної системи від часу часто виявляється зручним представляти у вигляді речовинної частини комплексного вираження
![]() (1,11)
(1,11)
де А — комплексна постійна; написавши її у вигляді
A = aeia , (1,12)
ми повернемося до вираження (1,8). Постійну А називають комплексною амплітудою ; її модуль збігається зі звичайною амплітудою, а аргумент — з початковою фазою.
Оперування з експонентними множниками в математичному відношенні простіше, ніж із тригонометричними, тому що диференціювання не міняє їхнього виду. При цьому поки ми робимо лише лінійні операції (додавання, множення на постійні коефіцієнти, диференціювання, інтегрування), можна взагалі опускати знак узяття речовинної частини, переходячи до останнього лише в остаточному результаті обчислень.
Змушені коливання
Перейдемо до розгляду коливань у системі, на якій діє деяке змінне зовнішнє поле; такі коливання називають змушеними на відміну від розглянутих так званих вільних коливань. Оскільки коливання передбачаються як і раніше малими, те тим самим мається на увазі, що зовнішнє поле досить слабке, у противному випадку воно могло б викликати занадто великий зсув х.
У цьому випадку поряд із власною потенційною енергією ½kx2 система має ще потенційну енергію Ue( x,t) , пов'язаної з дією зовнішнього поля. Розкладаючи цей додатковий член у ряд по ступенях малої величини х, одержимо:
![]()
Перший член є функцією тільки від часу й тому може бути опущений у лагранжевої функції (як повна похідна по t від деякої іншої функції часу). У другому члені — dUe/dx є зовнішня «сила», що діє на систему в положенні рівноваги заданою функцією часу; позначимо її як F(t) . Таким чином, у потенційній енергії з'являється член — xF(t) , так що функція Лагранжа системи буде:
![]() (2,1)
(2,1)
Відповідне рівняння руху є
![]()
або
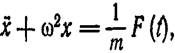 (2,2)
(2,2)
де ми знову ввели частоту з вільних коливань.
Як відомо, загальне рішення неоднорідного лінійного диференціального рівняння з постійними коефіцієнтами виходить у вигляді суми двох виражень: х = х0 + х1 , де х0 — загальне рішення однорідного рівняння, a х1 — приватний інтеграл неоднорідного рівняння. У цьому випадку х0 являє собою розглянуті вільні коливання.
Розглянемо особливий інтерес, що представляє, випадок, що коли змушує сила теж є простою періодичною функцією часу з деякою частотою в: