Курсовая работа: Опис та типологія коливань

Дослідження змушених коливань при наявності тертя цілком аналогічно зробленому в п. 1.2 змушені коливання. Ми зупинимося тут докладно на випадку, що представляє самостійний інтерес, періодичної сили, що змушує.

Додавши в правій стороні рівняння (4.1) зовнішню силу f cos yt і розділивши на т, одержимо рівняння руху у вигляді

(5.1)

Рішення цього рівняння зручно знаходити в комплексній формі, для чого пишемо в правій частині e^iγt замість cos yt:

Приватний інтеграл шукаємо у вигляді x = B e^iγt і знаходимо для В:

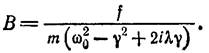(5.2)

Представивши В у виді be^iδ , маємо для b і δ:

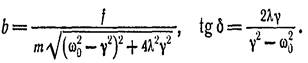(5.3)

Нарешті, відокремивши речовинну частину від вираження Be^iγt = be^i(γt+δ) , одержимо приватний інтеграл рівняння (5.1), а додавши до нього загальне рішення рівняння без правої частини (яке ми напишемо для визначеності для випадку ω0>?), одержимо остаточно:

х = ае^-λt cos (ωt+ a) + b cos (γt + δ). (5.4)

Перший доданок експоненціальне убуває згодом, так що через досить великий проміжок часу залишається тільки другий член:

x = b cos (γt + δ). (5.5)

Вираження (5.3) для амплітуди b змушеного коливання хоча й зростає при наближенні частоти γ до ω₀ , але не звертається в нескінченність, як це було при резонансі під час відсутності тертя. При заданій амплітуді сили f амплітуда коливання максимальна при частоті

при λ<<<ω₀ це значення відрізняється від ω₀ лише на величину другого порядку малості.

Розглянемо область поблизу резонансу. Покладемо γ = ω₀ + ε, де ε — мала величина; будемо також уважати, що λ<<ω₀ . Тоді в (5.2) можна приблизно замінити:

так що

(5.6)

або

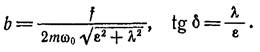(5.7)

Відзначимо характерну рису ходу зміни різниці фаз δ між коливанням і силою, що змушує, при зміні частоти останньої. Ця різниця завжди негативна, тобто коливання «запізнюється» щодо зовнішньої сили. Удалині від резонансу, з боку γ < ω₀ , δ прагне до нуля, а з боку γ > ω0 — до значення — π. Зміна δ від нуля до — π відбувається у вузькій (ширини ~ λ) області частот, близьких до ω0; через значення -π/2 різниця фаз проходить при γ = ω0. Відзначимо в цьому зв'язку, що під час відсутності тертя зміна фази змушеного коливання на величину ? відбувається стрибком при ? = ?0 (другий член в (2.4) міняє знак); облік тертя «розмазує» цей стрибок.

При усталеному русі, коли система робить змушені коливання (5.5), її енергія залишається незмінної. У той же час система безупинно поглинає (від джерела зовнішньої сили) енергію, що дисипарується завдяки наявності тертя. Позначимо за допомогою I(γ) кількість енергії, що поглинається в середньому в одиницю часу, як функцію частоти зовнішньої сили. Згідно (4.13) маємо: I (γ) = 2F ,

де F — середнє (по періоду коливання) значення дисипативної функції. Для одномірного руху вираження (4.11) дисипативної функції зводиться до

Підставивши сюди (5.5), одержимо:

Середнє за часом значення квадрата синуса дорівнює ? , тому