Курсовая работа: Ортогональные полиномы и кривые распределения вероятностей
следовательно, от его дискриминанта
![]()
который можно написать в виде
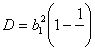 ,
,
вводя параметр
æ![]() .
.
Или иначе, величину æ можно представить в виде:
æ![]() ,
,
где величины ![]() представимы через центральные моменты статистических распределений
представимы через центральные моменты статистических распределений ![]() к-го порядка, которые определяются по формуле
к-го порядка, которые определяются по формуле
![]() ,
,
где ![]() есть
есть
![]() .
.
Тогда
![]() ,
, ![]() .
.
Через величины ![]() можно представить и величины
можно представить и величины ![]() следующим образом [5]:
следующим образом [5]:

Величина æ называется критерием Пирсона (каппа Пирсона) и различные значения ее дают нам следующие выводы о корнях уравнения:
А. Если æ![]() , то
, то ![]() и уравнение (1) имеет вещественные корни различных знаков.
и уравнение (1) имеет вещественные корни различных знаков.
В. Если 0< æ<1, то ![]() и уравнение (1) имеет комплексные корни.
и уравнение (1) имеет комплексные корни.
С. Если æ>1, то ![]() и уравнение (1) имеет вещественные корни одного знака.
и уравнение (1) имеет вещественные корни одного знака.
Соответственно этим случаям Пирсон различает три главных типа своих кривых, которые он назвал соответственно типами I, IV и VI. Затем æ может равняться ![]() , что дает переходные типы кривых. Наконец, присоединяя некоторые дополнительные условия, мы можем увеличить число переходных типов. Всего система кривых Пирсона заключает 12 типов и нормальную кривую.
, что дает переходные типы кривых. Наконец, присоединяя некоторые дополнительные условия, мы можем увеличить число переходных типов. Всего система кривых Пирсона заключает 12 типов и нормальную кривую.
В своих разработках Колмогоров А. Н. и Марков А. А. доказали, что любой закон распределения может быть записан в виде одного из двенадцати типов кривых Пирсона, поэтому для решения задачи идентификации используется метод Пирсона.
§ 2. Основные типы кривых Пирсона.
В этом параграфе будут рассмотрены основные типы кривых распределения вероятностей, предложенные и классифицированные Пирсоном.
Тип I.
Пусть æ<0. Тогда
![]()
и уравнение (2) имеет вещественные корни различных знаков: ![]() , так что можем записать
, так что можем записать
![]() .
.
Тогда правая часть уравнения (1) может быть представлена в виде: