Курсовая работа: Ортогональные полиномы и кривые распределения вероятностей

;

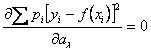После преобразований получаем следующую систему уравнений для нахождения коэффициентов

;

;

……………………

……………………

;

……………………

;

где

Такой подход к нахождению коэффициентов имеет существенный недостаток – при повышении степени полинома хотя бы на единицу приходится переписывать все уравнения и решать систему заново.

Есть другой вариант построения искомого полинома [8].

Пусть будет целая функция от степени , которая обращается в при . Положим

,

где - целые функции степеней , а - коэффициенты.

Пусть теперь сумма первых членов выражения

равняется

,

т.е. .

Каковы в этом случае условия относительно и при которых сумма

имеет наименьшее значение?

Обозначим эту сумму через :

,

и, подставляя в нее

,

составляем обычным способом дифференцирования следующие уравнения: