Курсовая работа: Ортогональные полиномы и кривые распределения вероятностей

и .

Функция станет равной , функции определяются путем последовательных подстановок выражений в формулы

.

При помощи этих формул можно вычислить какой угодно член ряда Чебышева

.

Оценка результатов интерполирования производится при помощи среднего квадратического отклонения данных значений интерполируемой функции от вычисленных по найденному уравнению параболы.

Обозначим сумму квадратов отклонений через . Тогда можно написать

.

будет равняться

,

а выражать рекуррентно через по формуле

.

Итак,

, , ,

, , , ,

, , , , .

Мы видим, что в зависимости от нашей весовой функции в разложении мы получим разные системы ортогональных полиномов.

§ 2. Обобщение Грамма - Шарлье.

Пусть по методу Пирсона найден вид кривой распределения вероятностей на соответствующем интервале. Теперь, для представления в удобном для практического использования виде, запишем полученную кривую в несколько иной форме. Для этого используем обобщение Грамма – Шарлье, которое основывается на применении ортогональных полиномов Чебышева и состоит в том, что кривая распределения вероятностей представима в виде следующего разложения:

(4)

где - есть к–ая производная функции . Здесь полагаем, что

.

Таким образом, мы получаем кривую распределения вероятностей теперь уже в виде .

Производные функции мы можем представить в виде [3]

,

тогда можем записать

где функции должны удовлетворять следующему свойству:

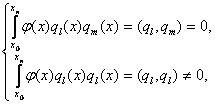если (5)

А коэффициенты получаются из равенства (4) с помощью домножения на любой из ортогональных полиномов и, интегрирования полученного равенства: