Курсовая работа: Ортогональные полиномы и кривые распределения вероятностей

,

получается при

æ.

Кривая простирается от до , начало координат в точке и

.

Тип N.

Тринадцатый тип кривых распределения Пирсона – нормальная кривая с уравнением

,

которая получается при условиях

æ.

Типы II, VI, VII, VIII, IX представляют специальные случаи кривой типа I, тип X – специальный случай типа III, а тип XI - типа VI. [5] (См. приложение 1.)

Глава 2. Применение ортогональных полиномов Чебышева при нахождении кривых распределения вероятностей.

В этой главе рассмотрено получение ортогональных полиномов способом, который разработал П. Л. Чебышев. А именно, через разложение в непрерывную дробь суммы

и рассмотрение знаменателей подходящих дробей полученной непрерывной дроби. Причем показано, что полученные таким образом ортогональные полиномы отвечают условиям метода наименьших квадратов, а так же показано их применение для нахождения кривых распределения вероятностей.

§ 1. Получение ортогональных полиномов по способу Чебышева.

Пусть даны значения интерполируемой функции,

соответствующие значения аргумента . Каждому значению аргумента ставится в соответствие частота .

Требуется найти такую целую функцию

,

где , которая удовлетворяла бы условию наименьшего значения суммы

.

В данной задаче в качестве веса предлагается рассмотреть [8]

,

где n есть

или иначе говоря n - сумма всех испытаний.

Для решения нашей задачи находим коэффициенты , которые определяются из следующих уравнений

;

;

……………………
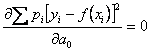
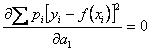