Курсовая работа: Ортогональные полиномы и кривые распределения вероятностей

,

Когда найдены и , и находятся по формулам

,

в которых

, .

Здесь использовано равенство

,

которое получается, так мы имеем

,

и

,

следовательно,

,

откуда

(так как ), нужно брать .

Таким образам, и есть корни уравнения

и и по формулам

,

в которых

,

где находится из равенства

.

Остается найти . Оно находится по равенству

.

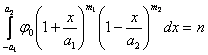При помощи подстановки

мы находим: