Курсовая работа: Ортогональные полиномы и кривые распределения вероятностей

Следовательно,

.

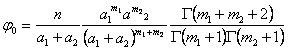Тип IV.

Второй главный тип кривых Пирсона, соответствующий значениям

0< æ<1, когда уравнение (1) имеет комплексные корни.

Пусть эти корни равны

,

где

.

Тогда уравнение (1) будет

,

откуда

,

и

,

или

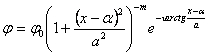,(3)

причем

.

Параметры кривой (3), выражаются следующим образом через моменты и константы :

(здесь , и ),

,

где - функция Пирсона, определяемая равенством

.

Интеграл в правой части можно привести к другому виду:

подстановка

приводит его к виду