Курсовая работа: Ортогональные полиномы и кривые распределения вероятностей

Обычно, полагая

,

пишут в виде

,

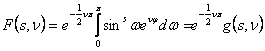где

.

Тип VI.

Третий главный тип кривых Пирсона, соответствующий значениям критерия æ>1 . В этом случае уравнение (2) имеет вещественные корни одного знака. Не приводя вывода уравнения кривой типа VI, аналогичного выводу уравнения кривой типа I [5], прямо приведем уравнение, отнесенное к средней выравниваемого распределения, как началу координат:

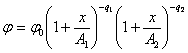
(в нем ). Его параметры вычисляются по формулам:

,

причем берется , если и , если ; и дают выражения:

,

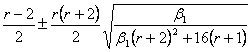причем должно быть ;

,

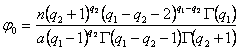и

.

Уравнение кривой типа VI пишут также в виде:

беря за начало координат точку

.

Параметры вычисляются как выше, а имеет теперь такое выражение:

.

Кривая простирается от до , если , и от до , если .

§ 3. Переходные типы кривых Пирсона.

Переходные типы кривых Пирсона получаются при специальных значениях критерия æ и при некоторых условиях, налагаемых на и .

Тип II.

Получается при æ=0, и имеет уравнение

,

отнесенное к моде, которая теперь равна средней (кривая симметрична относительно начала). Ее параметры вычисляются по формулам