Курсовая работа: Ортогональные полиномы и кривые распределения вероятностей

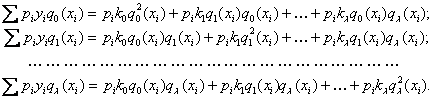
Так как есть ортогональные полиномы по построению, следовательно все слагаемые вида будут равняться 0.

В результате преобразований получим выражения для коэффициентов :

;

;

………………

;

………………

.

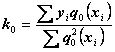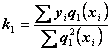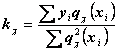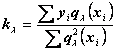Теперь можно представить функцию

в таком виде

.

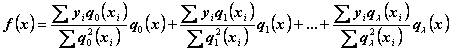Легко убедиться, что для перехода от найденного выражения интерполируемой функции к целой функции степени , достаточно к левой части полученной функции приписать один новый член

.

Для дальнейшего перехода к целой функции степени , также удовлетворяющей условию наименьшего значения суммы

,

достаточно прибавить к найденному выражению функции степени , такой новый член

.

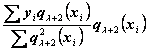Таким образом, решение задачи параболического интерполирования по способу наименьших квадратов приводится к нахождению ряда

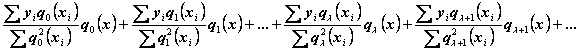
Этот ряд, обладающий свойством давать посредством суммы своих первых членов приближенное представление интерполируемой функции в виде целой функции степени , удовлетворяющей требованию наименьших квадратов, называется интерполяционным рядом Чебышева.

Теперь для полного решения задачи остается еще узнать, что представляют собой функции , определив через данные величины и коэффициенты при в выражении этих функций.

Далее, с помощью разложения дроби

по нисходящим степеням получим, что дробь

,

где

,