Курсовая работа: Особые свойства Гамма-функции Эйлера

Тогда уравнение (2.1) для образа гамма-функции имеет вид:

Это уравнение легко решить:

(2.2)

Нетрудно заметить, что найденная функция [(Г)\tilde](p) на самом деле такова, что внеинтегральный член в формуле (2.2) равен нулю.

Зная образ гамма-функции, легко получить и выражение для прообраза:

Это неканоническая формула, для того, чтобы привести ее к виду, полученному Эйлером, надо сделать замену переменной интегрирования: t = exp(-p), тогда интеграл примет вид:

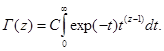
Постоянная C выбирается так, чтобы при целых значениях z гамма-функция совпадала с функцией факториал: Г(n+1) = n!, тогда:

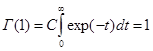
следовательно C = 1. Окончательно, получаем формулу Эйлера для гамма-функции:

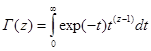
(2.3)

Эта функция очень часто встречается в математических текстах. При работе со специальными функциями, пожалуй, даже чаще, чем восклицательный знак.

Проверить, что функция, определенная формулой (2.3), действительно удовлетворяет уравнению (2.1), можно, проинтегрировав интеграл в правой части этой формулы по частям:

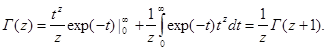
2.3 Область определения и полюсы

В подынтегральной функции интеграла (2.3) при экспонента exp(-tz ) при R(z ) > 0 убывает гораздо быстрее, чем растет алгебраическая функция t ^(z-1) . Особенность в нуле - интегрируемая, поэтому несобственный интеграл в (2.3) сходится абсолютно и равномерно при R (z) > 0. Более того, последовательным дифференцированием по параметру z легко убедиться, что Г(z ) - голоморфная функция при R (z ) > 0. Однако, непригодность интегрального представления (2.3) при R (z ) 0 не означает, что там не определена сама гамма-функция - решение уравнения (2.1).

Рассмотрим поведение Г(z) в окрестности нуля. Для этого представим:

где - голоморфная функция в окрестности z = 0 . Из формулы (2.1) следует:

Тогда

то есть Г(z) имеет полюс первого порядка при z = 0.

Также легко получить: