Курсовая работа: Особые свойства Гамма-функции Эйлера
Чтобы выяснить значение постоянной, вспомним, что I(1) = 1, с другой стороны:
![]()
Интегральное представление
![]()
(2.5)
называется представлением Ганкеля по петле.
Легко видеть, что функция 1/Г(z ) не имеет полюсов в комплексной плоскости, следовательно, гамма-функция не имеет нулей.
С помощью этого интегрального представления можно получить формулу для произведения гамма-функций. Для этого в интеграле сделаем замену переменной ![]() , тогда:
, тогда:
![]()
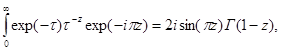
то есть
![]()
2.5 Предельная форма Эйлера
Гамма-функцию можно представить в виде бесконечного произведения. Это можно заметить, если в интеграле (2.3) представить
![]()
Тогда интегральное представление гамма-функции:
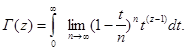
В этой формуле мы можем поменять пределы - предел интегрирования в несобственном интеграле и предел при ![]() внутри интеграла. Приведем результат:
внутри интеграла. Приведем результат:
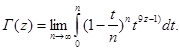
Возьмем по частям этот интеграл:
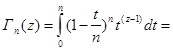
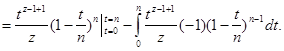
![]()
Если провести эту процедуру n раз, получим:
![]()
Переходя к пределу, получим предельную форму Эйлера для гамма-функции:
![]()
(2.6)
2.6 Формула для произведения