Курсовая работа: Особые свойства Гамма-функции Эйлера

то есть в окрестности точки функция Г(z ) также имеет полюс первого порядка.

Таким же образом можно получить формулу:

(2.4)

Из этой формулы следует, что точки z = 0,-1,-2,... - простые полюсы гамма-функции и других полюсов на вещественной оси эта функция не имеет. Нетрудно вычислить вычет в точке z = -n, n = 0,1,2,...:

2.4 Представление Ганкеля через интеграл по петле

Выясним, имеет ли гамма-функция нули. Для этого рассмотрим функцию

Полюсы этой функции и есть нули функции Г(z).

Разностное уравнение для I(z ) легко получить, воспользовавшись выражением для Г(z ):

Выражение для решения этого уравнения в виде интеграла можно получить так же, как было получено интегральное выражение для гамма-функции - через преобразование Лапласа. Ниже приведены вычисления.ни такие же, как и в п.1).ии теграла будут точки ____________________________________________________________________________

или

После разделения переменных получим:

Проинтегрировав получаем:

или

Переход к прообразу Лапласа дает:

В полученном интеграле сделаем замену переменной интегрирования:

тогда

Здесь важно заметить, что подынтегральная функция при нецелых значениях z имеет точку ветвления t = 0. На комплексной плоскости переменной t проведем разрез по отрицательной вещественной полуоси. Интеграл по этой полуоси представим как сумму интеграла по верхнему берегу этого разреза от до 0 и интеграла от 0 до по нижнему берегу разреза. Чтобы интеграл не проходил через точку ветвления, устроим вокруг нее петлю.

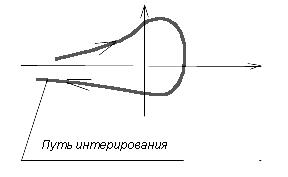
Рис1: Петля в интегральном представлении Ганкеля.

В результате получим: