Изучим теперь поведение - функции и построим эскиз ее графика. (см. Приложение 1)

Из выражения для второй производной -функции видно, что для всех . Следовательно, возрастает. Поскольку , то по теореме Роля на сегменте [1,2]производная при и при , т. е. Монотонно убывает на и монотонно возрастает на . Далее , поскольку , то при . При из формулы следует , что при .

Равенство , справедливое при , можно использовать при распространении - функции на отрицательное значение .

Положим для, что . Правая часть этого равенства определена для из (-1,0) . Получаем, что так продолженная функция принимает на (-1,0) отрицательные значения и при , а также при функция .

Определив таким образом на , мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением окажется функция, принимающая положительные значения и такая, что при и . Продолжая этот процесс, определим функцию , имеющею разрывы в целочисленных точках (см. Приложение 1.)

Отметим еще раз, что интеграл

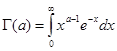
определяет Г-функцию только при положительных значениях , продолжение на отрицательные значения осуществлено нами формально с помощью формулы приведения .

4. Вычисление некоторых интегралов.

Формула Стирлинга

Применим гамма функцию к вычислению интеграла:

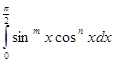
где m > -1,n > -1.Полагая , что ,имеем

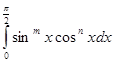
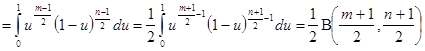
и на основании (2.8) имеем

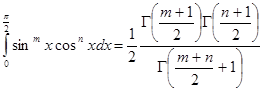
(4.1)

В интеграле

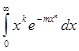
Где k > -1,n > 0,достаточно положить

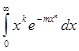
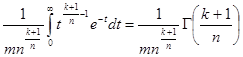
Интеграл

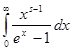
Где s > 0,разложить в ряд

=

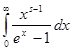
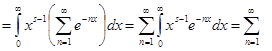
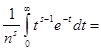
где дзетта функция Римана

Рассмотрим неполные гамма функции (функции Прима)