Курсовая работа: Приближенное решение интегрального уравнения
Запишем таблицу значений функций ![]()
| i | |||
| 0 | 0 | 0 | 0 |
| 1 | 0,1 | -0,2 | 0,03 |
| 2 | 0,2 | -0,4 | 0,12 |
| 3 | 0,3 | -0,6 | 0,27 |
| 4 | 0,4 | -0,8 | 0,48 |
| 5 | 0,5 | -1 | 0,75 |
| 6 | 0,6 | -1,2 | 1,08 |
| 7 | 0,7 | -1,4 | 1,47 |
| 8 | 0,8 | -1,6 | 1,92 |
| 9 | 0,9 | -1,8 | 2,43 |
| 10 | 1 | -2 | 3 |
1. Метод конечных разностей для линейных дифференциальных уравнений второго порядка.
1. Пусть ![]() и значения
и значения ![]() и
и ![]() в каждом узле можно записать конечно-разностными отношениями
в каждом узле можно записать конечно-разностными отношениями
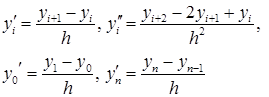 (3)
(3)
тогда, используя (3), заменим уравнения (1), (2) системой
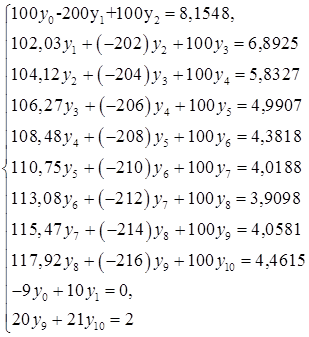 (4)
(4)
Решая систему (4), получим
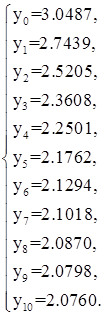
2. Пусть ![]() тогда, используя (3), заменим уравнения (1), (2) системой:
тогда, используя (3), заменим уравнения (1), (2) системой:
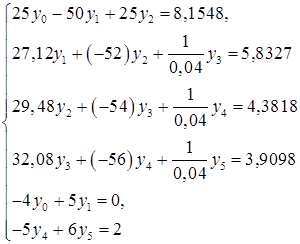 (5)
(5)
Решая систему (5), получим
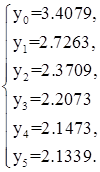
2. Метод центральных разностей для линейных дифференциальных уравнений второго порядка.
1. Пусть ![]() и значения
и значения ![]() и
и ![]() в каждом узле можно записать центрально-разностными отношениями
в каждом узле можно записать центрально-разностными отношениями
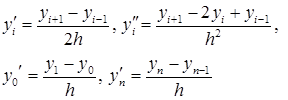 (6)
(6)
тогда, используя (6), заменим уравнения (1), (2) системой:
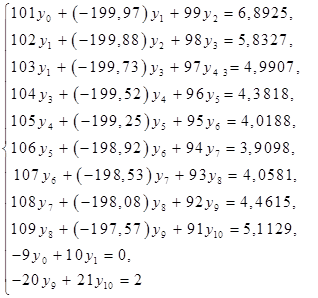 (7)
(7)
Решая систему (7), получим:
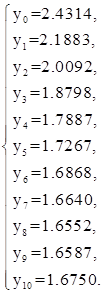
2. Пусть ![]() , тогда, используя (6), заменим уравнения (1), (2) системой:
, тогда, используя (6), заменим уравнения (1), (2) системой:
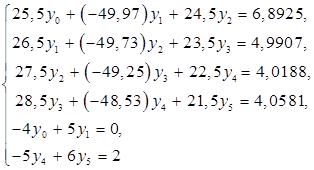 (8)
(8)
Решая систему (8), получим
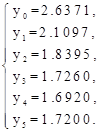
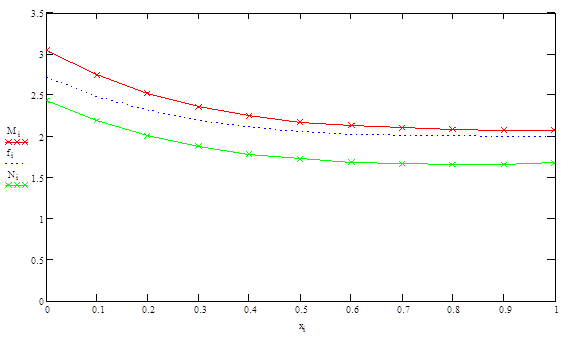
Рис.1-![]() - решение, полученное с помощью метода конечных разностей (h=0,1),
- решение, полученное с помощью метода конечных разностей (h=0,1), ![]() - решение, полученное с помощью метода центральных разностей (h=0,1),
- решение, полученное с помощью метода центральных разностей (h=0,1), ![]() - точное решение
- точное решение
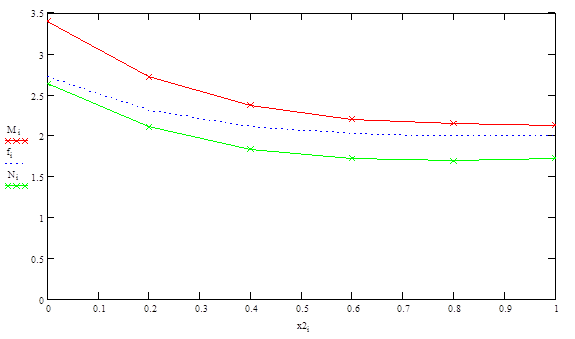
Рис.2-![]() - решение, полученное с помощью метода конечных разностей (h=0,2),
- решение, полученное с помощью метода конечных разностей (h=0,2), ![]() - решение , полученное с помощью метода центральных разностей (h=0,2)
- решение , полученное с помощью метода центральных разностей (h=0,2) ![]() -точное решение
-точное решение
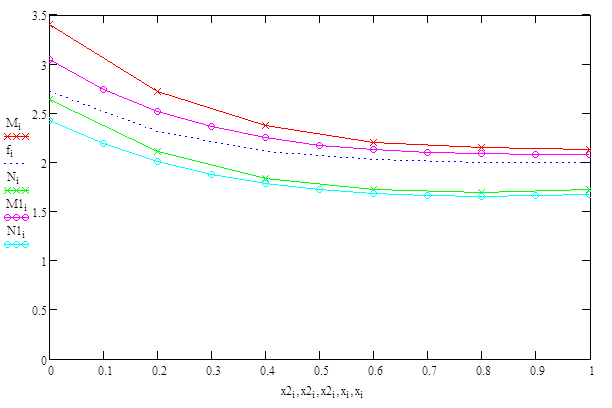
Рис.3- Общий график решений