Курсовая работа: Приближенное решение интегрального уравнения
Конечно-разностные отношения в методе прогонки.
1. Пусть 
и значения 
и 
в каждом узле можно записать конечно-разностными отношениями:
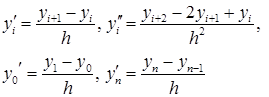(9)
тогда, используя (20), заменим уравнения (1), (2), (3) системой:
(10)
Запишем первые n-1 уравнений в виде:
, где 
(11)
Из системы (21) следует, что 
(12)
, 
вычисляются последовательно, но при i=0:
(13)
Остальные , вычисляются по формуле:
(14)
Прямой ход вычислений.
По формулам (11) вычисляем 
. Далее вычисляем 
по формулам (13) и по рекуррентным формулам (14) находим 
.
Обратный ход.
Из уравнения (12) при i=n-2 и из последнего уравнения системы (10) получаем:
Решив эту систему относительно 
, получим
(15)
При i=n-2,…,1 используем формулу (12)
вычисляем из второго уравнения системы (10)
(16)
В результате вычислений получим таблицу:
Таблица №1
| Прямой ход | Обратный ход | ||||||||
| i | xi | pi | qi | fi | mi | ki | ci | di | yi |
| 0 | 0 | 0 | 0 | 8.1548 | -2 | 1 | -1.125 | 0.081548 | 3.049606 |
| 1 | 0.1 | -0.2 | 0.03 | 6.9025 | -2.02 | 1.0203 | -1.14658 | 0.162629 | 2.744645 |
| 2 | 0.2 | -0.4 | 0.12 | 5.8327 | -2.04 | 1.0412 | -1.18177 | 0.252476 | 2.521233 |
| 3 | 0.3 | -0.6 | 0.27 | 4.9907 | -2.06 | 1.0627 | -1.24358 | 0.366984 | 2.361553 |
| 4 | 0.4 | -0.8 | 0.48 | 4.3818 | -2.08 | 1.0848 | -1.36806 | 0.538893 | 2.250789 |
| 5 | 0.5 | -1 | 0.75 | 4.0188 | -2.1 | 1.1075 | -1.70977 | 0.856677 | 2.176909 |
| 6 | 0.6 | -1.2 | 1.08 | 3.9098 | -2.12 | 1.1308 | -5.35913 | 1.695401 | 2.130132 |
| 7 | 0.7 | -1.4 | 1.47 | 4.0581 | -2.14 | 1.1547 | 0.247024 | 10.53205 | 2.10254 |
| 8 | 0.8 | -1.6 | 1.92 | 4.4615 | -2.16 | 1.1792 | -0.40795 | -3.02327 | 2.087729 |
| 9 | 0.9 | -1.8 | 2.43 | 5.1129 | -2.18 | 1.2043 | -0.59217 | -1.43418 | 2.080518 |
| 10 | 1 | -2 | 3 | 6 | -2.2 | 1.23 | -0.67952 | -0.98461 | 2.076684 |
2. Пусть 
В результате вычислений по формулам (9)-(16) получим таблицу:
Таблица №2
| Прямой ход | Обратный ход | ||||||||
| i | xi | pi | qi | fi | mi | ki | ci | di | yi |
| 0 | 0 | 0 | 0 | 8.1548 | -2 | 1 | -1.125 | 0.081548 | 2.048941 |
| 1 | 0.2 | -0.4 | 0.12 | 5.8327 | -2.04 | 1.0412 | -1.15121 | 0.156074 | 1.844047 |
| 2 | 0.4 | -0.8 | 0.48 | 4.3818 | -2.08 | 1.0848 | -1.20313 | 0.247519 | 1.720701 |
| 3 | 0.6 | -1.2 | 1.08 | 3.9098 | -2.12 | 1.1308 | -1.31665 | 0.407622 | 1.650761 |
| 4 | 0.8 | -1.6 | 1.92 | 4.4615 | -2.16 | 1.1792 | -1.64636 | 0.835965 | 1.619574 |
| 5 | 1 | -2 | 3 | 6 | -2.2 | 1.23 | -5.71492 | 5.936293 | 1.63769 |
