Курсовая работа: Приближенное решение интегрального уравнения

Применяя метод сеток с шагом , найти решение задачи Дирихле в квадрате с вершинами А(0,0), В(0,1), С(1,1), D(1,0).

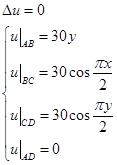(20)

1. Метод Либмана

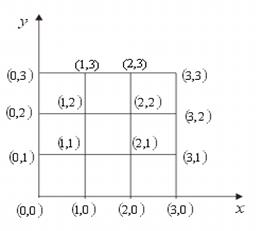
Найдем значения функции в каждом узле:

На АВ

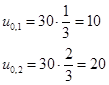
На ВС

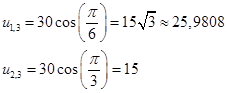
На СD

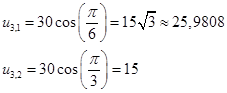
На АD

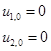
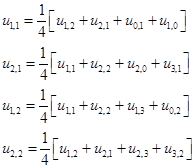
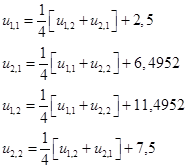
Запишем формулу метода последовательных приближений

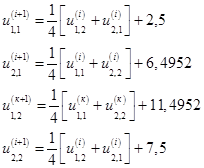
Пусть , тогда получим

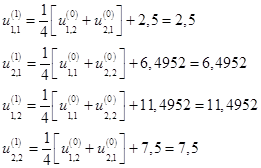
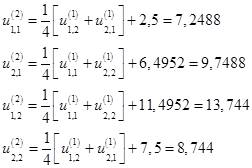
Таблица №3

i	u1 , 1	u1 , 2	u2 , 1	u2 , 2
0	0	0	0	0
1	2,5	11,4952	7,5	6,4952
2	7,2488	13,744	9,7488	8,744
3	8,3732	15,4934	11,4982	10,4934
4	9,2479	16,21185	12,21665	11,21185
5	9,607125	16,61014	12,61494	11,61014
6	9,806269	16,79952	12,80432	11,79952
7	9,900958	16,89665	12,90145	11,89665

2. Метод Гаусса

Для нахождения точного решения задачи (20) используем метод Гаусса. Для этого решим систему

линейный дифференциальный уравнение

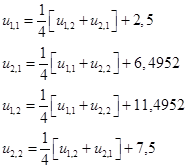(20*)

Введем замену