Курсовая работа: Приближенное решение интегрального уравнения

Составим невязку

На отрезке [-π, π] выберем две точки коллокации: 0 и . Составим систему уравнений

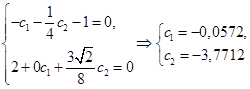
Таким образом, решение задачи (17)

3. Метод Ритца

Составим функционал по формуле

(19)

На отрезке [a, b] выберем систему базисных функций

Будем искать решение задачи (17) в виде

Подставим в (19)

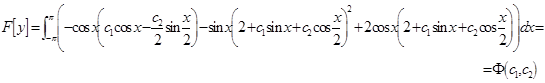
Составим систему уравнений относительно с₁ , с₂

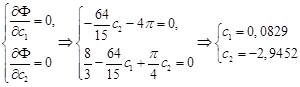
Таким образом, решение задачи (17)

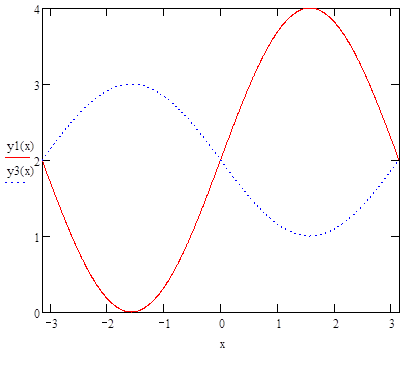
Рис.4- у1(х)-решение, полученное с помощью метода Галеркина (две базисные функции), у2(х)-решение, полученное с помощью метода коллокации (две базисные функции)

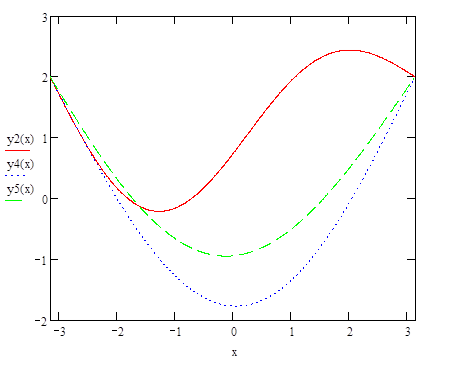
Рис.4-у2(х)- решение, полученное с помощью метода Галеркина (три базисные функции), у4(х)- решение, полученное с помощью метода коллокации (три базисные функции), у5(х)- решение, полученное с помощью метода Ритца (три базисные функции)

Замечание: найти решение методом Ритца для двух базисных функций не удалось, т.к. функция Ф(с₁ ) не квадратична относительно переменной с₁ и не удовлетворяет условию существования экстремума