Курсовая работа: Приближенное решение интегрального уравнения
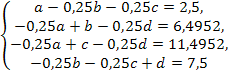
Решая систему, получим
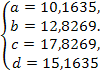
Таким образом, получим точное решение задачи (20)
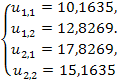
IV. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ПЕРВОЙ СМЕШАННОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ОТРЕЗКЕ
Пусть дано уравнение теплопроводности и его граничные условия
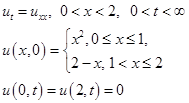 (21)
(21)
Решим задачу (21), применяя метод сеток для уравнений параболического типа.
1. Пусть ![]() , тогда l=0,02- шаг по оси t, а h=0,2- шаг по оси x. Решение будем искать в виде
, тогда l=0,02- шаг по оси t, а h=0,2- шаг по оси x. Решение будем искать в виде
![]() (22)
(22)
где ![]() (23)
(23)
Получим таблицу:
Таблица №4
| j | tj /xi | 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 |
| 0 | 0 | 0 | 0,04 | 0,16 | 0,36 | 0,64 | 1 |
| 1 | 0,02 | 0 | 0,08 | 0,2 | 0,4 | 0,68 | 0,72 |
| 2 | 0,04 | 0 | 0,1 | 0,24 | 0,44 | 0,56 | 0,74 |
| 3 | 0,06 | 0 | 0,12 | 0,27 | 0,4 | 0,59 | 0,61 |
| 4 | 0,08 | 0 | 0,135 | 0,26 | 0,43 | 0,505 | 0,63 |
| 5 | 0,1 | 0 | 0,13 | 0,2825 | 0,3825 | 0,53 | 0,5375 |
| j | tj /xi | 1,2 | 1,4 | 1,6 | 1,8 | 2 | |
| 0 | 0 | 0,8 | 0,6 | 0,4 | 0,2 | 0 | |
| 1 | 0,02 | 0,8 | 0,6 | 0,4 | 0,2 | 0 | |
| 2 | 0,04 | 0,66 | 0,6 | 0,4 | 0,2 | 0 | |
| 3 | 0,06 | 0,67 | 0,53 | 0,4 | 0,2 | 0 | |
| 4 | 0,08 | 0,57 | 0,535 | 0,365 | 0,2 | 0 | |
| 5 | 0,1 | 0,5825 | 0,4675 | 0,3675 | 0,1825 | 0 |
2. Пусть ![]() , тогда l=0,015- шаг по оси t, а h=0,3- шаг по оси x. Решение в виде (22) будем искать по формуле
, тогда l=0,015- шаг по оси t, а h=0,3- шаг по оси x. Решение в виде (22) будем искать по формуле
![]() (24)
(24)
В результате получим таблицу
Таблица №5
| j | tj /xi | 0 | 0,3 | 0,6 | 0,9 | 1,2 | 1,5 | 1,8 | 2 |
| 0 | 0 | 0 | 0,09 | 0,36 | 0,81 | 0,8 | 0,5 | 0,2 | 0 |
| 1 | 0,015 | 0 | 0,12 | 0,39 | 0,733333 | 0,751667 | 0,5 | 0,216667 | 0 |
| 2 | 0,03 | 0 | 0,145 | 0,402222 | 0,679167 | 0,706667 | 0,494722 | 0,227778 | 0 |
| 3 | 0,045 | 0 | 0,163704 | 0,405509 | 0,637593 | 0,666759 | 0,485556 | 0,234306 | 0 |
| 4 | 0,06 | 0 | 0,176721 | 0,403889 | 0,603773 | 0,631698 | 0,473881 | 0,23713 | 0 |
| 5 | 0,075 | 0 | 0,185129 | 0,399342 | 0,575113 | 0,600741 | 0,460725 | 0,237067 | 0 |
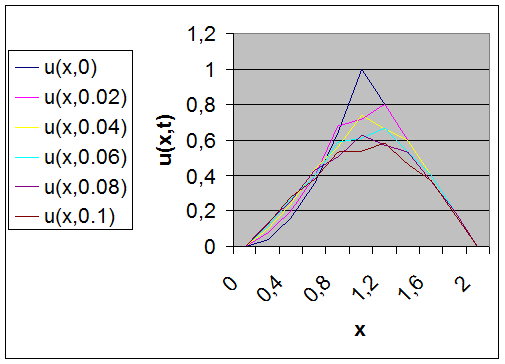
Рис.5- Решение, полученное с помощью метода сеток при
![]()
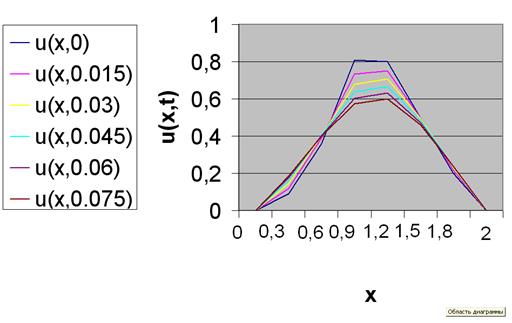
Рис.6- Решение, полученное с помощью метода сеток при
![]()

Рис.7- График точного решения, полученного аналитически
V. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ПЕРВОЙ СМЕШАННОЙ ЗАДАЧИ ДЛЯ ВОЛНОВОГО УРАВНЕНИЯ НА ОТРЕЗКЕ
Пусть дано волновое уравнение и его граничные условия
 (25)
(25)