Курсовая работа: Применение производной при нахождении предела
Геометрическая интерпретация
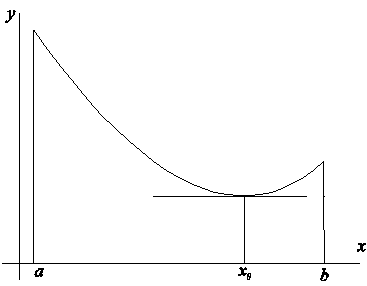
2.2 Теорема Ролля о нуле производной
Теорема. Если f непрерывна на [a,b], дифференцируема на (a,b) и f (a) =f (b). Тогда
$ x0 Î (a,b): f ¢ (x0 ) =0 .
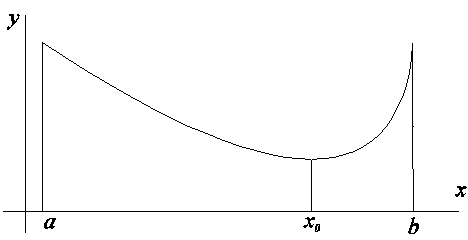
Доказательство. Положим
![]() ,
, ![]() .
.
Хотя бы одна из точек x1 , x2 внутренняя и для этой точки утверждение следует из теоремы Ферма.
2.3 Теорема Лагранжа о конечных приращениях
Теорема. Если f непрерывна на [a,b], дифференцируема на (a,b), то
$ x Î (a,b): f (b) - f (a) =f ¢ ( x) (b-a).
Доказательство. Рассмотрим функцию
![]() .
.
Для этой функции F (a) =F (b) =0, и к ней применима теорема Роля
![]() .
.
Геометрическая интерпретация

Существует точка, касательная в которой, параллельна хорде, соединяющей точки A и B графика.
Следствие 1 . Если f непрерывна на [a,b], дифференцируема на (a,b) и f ¢ (x) º0 на (a,b), то f (x) ºconst.
Применяя теорему к произвольному отрезку [x0 ,x], где x0 произвольная фиксированная точка, получим
f (x) - f (x0 ) =f ¢ ( x ) (x - x0 ) =0, т.е. f (x) = f (x0 ).
Следствие 2 . Если f непрерывна на [a,b], дифференцируема на (a,b) и f ¢ (x) =g ¢ (x) на (a,b), то f (x) =g (x) + const .
2.4 Теорема Коши о конечных приращениях
Теорема. Если f, g непрерывны на [a,b], дифференцируемы на (a,b), то существует
x Î (a,b): g ¢ ( x ) (f (b) - f (a)) = f ¢ ( x ) (g (b) - g (a)).
Доказательство. Рассмотрим вспомогательную функцию
F (x) = g (x) (f (b) - f (a)) - f (x) (g (b) - g (a)).
Для этой функции
F (a) = g (a) (f (b) - f (a)) - f (a) (g (b) - g (a)) = g (a) f (b) - f (a) g (b),
F (b) = g (b) (f (b) - f (a)) - f (b) (g (b) - g (a)) = - f (a) g (b) +g (a) f (b),
таким образом, F ( a) = F ( b) и к ней применима теорема Ролля: существует точка x Î (a,b) для которой выполняется равенство