Курсовая работа: Применение производной при нахождении предела
то 
Лемма. Если
, (2)
то bk =0, k=0,1,…,n
Доказательство . в (2) перейдем к пределу при x ® x0 , получим
b0 = 0, 
,
делим полученное выражение на (x-x0 ) и переходим к пределу при x ® x0 и т.д.
Доказательство теоремы .
откуда и следует утверждение.
4.3 Другие формы остатка в формуле Тейлора
Пусть функция f (x) (n+1) - раз дифференцируема в окрестности Ua (x0 ) = (x0 -a,x0 +a) и y (x) дифференцируема в 
, y ¢ ¹0 в 
, y (x) непрерывна в .
Возьмем x Î (x0 -a,x0 +a), x ¹x0 и фиксируем. Для определенности будем считать x0 <x и рассмотрим на [x0 ,x] функцию
.
Отметим следующие свойства этой функции
j (x) =0
j (x0 ) =Rn (x)
j (z) непрерывна на [x0 ,x], дифференцируема на (x0 ,x).
Не очевидным является только четвертое свойство
=
=
=
.
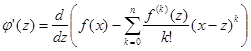К функциям j и y применим теорему Коши о конечных приращениях на отрезке [x0 ,x]
. Откуда 
и, далее,
(1)
Следствие 1 . Если функция f (n+1) - раз дифференцируема на (x0 -a, x0 +a), то
,
где x Î (x0 ,x) (или (x,x0 )),p>0. Остаток Шлемильха-Роша.
Для доказательства этой формулы следует в качестве функцииy (z) взять
y (z) = (x-z) p .
Следствие 2. (Формула Тейлора с остатком в форме Лагранжа) Если f (n+1) -раз дифференцируема на (x0 -a, x0 +a), то