Курсовая работа: Применение производной при нахождении предела

k = 2l+1,

Таким образом,

Следствие.

Пример 7. Используя следствие из предыдущего примера, найти предел (1401)

.

Имеем:

=|x|= sign x +o ().

Пример 8. Разложить функцию

f (x) =

по формуле Тейлора с остатком Пиано по степеням x до x⁴ включительно.

Сначала выпишем разложение функции по степеням x до x³ включительно.

Положим u=x - x² , тогда

= =1+ u+ u² + u³ + o ( u³ ) =1+ x - x² + ( x- x² ) ² + ( x- x² ) ³ + o ( x³ ) =1+ x- x³ + o ( x³ ).

Далее,

= =1+2 x (1+ x- x³ + o ( x³ )) =1+2 x+2 x² -2 x⁴ + o ( x⁴ ).

Второй способ. Так как

,

то на первом шаге выделяем единицу:

=.

Второе слагаемое представляем в виде Cxⁿ g₂ (x) так, чтобы , после чего следует представить функцию g₂ (x) в виде g₂ (x) = 1+g₃ (x) и т.д. В нашем случае:

====

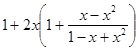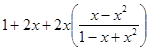==1+2x+=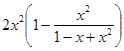

1+2x+2x² =1+2x+2x² -2x⁴ +o (x⁴ ).

4.6 Формула Тейлора для четных и нечетных функций

Теорема 1. Если функция f (x) четна и существует f ^{(2n+1) (} 0), то имеет место следующее разложение этой функции

.

Если функция f (x) нечетна и существует f ^{(2n+2) (} 0), то имеет место следующее разложение этой функции

.

Теорема 2. Если функция f (x) четна и существует f ^{(2n+2) (} x) в некоторой окрестности U (0), то для x ÎU (0) справедливо равенство