Курсовая работа: Применение производной при нахождении предела

=, x ®0,

выберем m=2n+1, тогда

cos x =, x ®0,

откуда, с учетом равенства f ^{(2n+1) (} 0) =0 , получаем разложение для косинуса

cos x =, x ®0

В формуле Тейлора с остатком Лагранжа

cos x =, x Î (0,x) ( или x Î (x,0)).

Действительно,

cos x =

===.

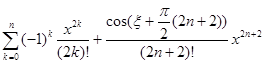Откуда следует, что

ln (1+x), x₀ =0

, x ®0

(1+x) ^a , x₀ =0,

интерес представляет случай, когдаa не является натуральным числом.

f ¢= a (1+x) ^a-1 ,…,f ^(k) = a ( a - 1) … ( a - k+1) (1+x) ^{a - k}

, x ®0

Важный частный случай

==.

4.5 Примеры использования стандартных разложений для представления функций по формуле Тейлора и для вычисления пределов

Из формул Тейлора следуют известные "равносильности при "; например,

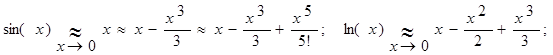
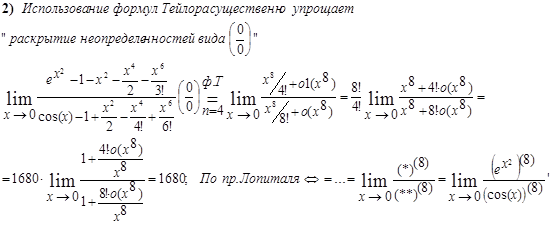
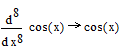
Пример 1.

Пример 2.

.