Курсовая работа: Применение производной при нахождении предела
Получено из общей формулы при p=n+1 .
Замечание . Формулу с остатком Лагранжа можно представить в виде.
.
Следствие 3 . Если f (n+1) -раз дифференцируема на (x0 -a, x0 +a), то справедлива формула Тейлора с остатком в форме Коши
Получено из общей формулы при p=1.
4.4 Разложение некоторых элементарных функций по формуле Тейлора
ex , x0 =0
,x Î (0,x),
если x>0 или x Î (x,0) в случае x <0.
Например, при |x|<1, |Rn (x) | £
sin x, x0 =0
Вспомогательная формула:
sin x = 
=
, x ®0,
выберем m=2n+2, тогда
sin x =
, x ®0,
откуда, с учетом равенства f (2n+2) ( 0) =0 , получаем разложение для синуса
sin x =
, x ®0
В формуле Тейлора с остатком Лагранжа
sin x =
, x Î (0,x) ( или x Î (x,0)).
Действительно,
sin x =
=
=
=
.
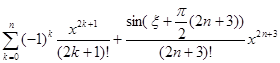Откуда следует, что
cos x, x0 =0
Вспомогательная формула:
