Курсовая работа: Применение производной при нахождении предела

Следствие. Если g ¢ (x) ¹0 на (a,b), то

.

Доказательство . Если g ¢ (x) ¹0, то g (b) - g (a) ¹0. Иначе, в случае g (b) =g (a), по теореме Ролля нашлась бы точка x, где g ¢ ( x) =0.

3. Раскрытие неопределенностей. правило лопиталя

3.1 Раскрытие неопределенностей вида 0/0

Дано: f (x), g (x) определены на (x₀ ,b) и

1)

2) f,g дифференцируемы на (x₀ ,b)

3) g ¢ (x) ¹0 на (x₀ ,b).

Тогда

,

если существует конечный или бесконечный предел

.

Доказательство . Доопределим f, g в точке x₀ по непрерывности нулем f (x₀ ) =g (x₀ ) =0 . По тереме Коши, примененной к отрезку [x₀ ,x], будет существовать x (x) Î (x₀ ,x): x₀ < x (x) < x и , из условия x₀ < x (x) <x следует, что , причем x (x) ¹x₀ , если x ¹x₀ . По теореме о существовании предела суперпозиции

= ч. т.д.

Замечание. Аналогично это утверждение доказывается для левой окрестности. Откуда получаем утверждение для x ® x₀ .

Следствие 1 . Если

1) Существуют f ^(k), g ^(k), k=1,2,…,n на (x₀ ,b)

2) , k=0,1,…,n-1

3) Существуeт g ^{(n) (} x) ¹0 на (x₀ ,b), то

,

если

существует, конечный или бесконечный.

Следствие 2 . Если f, g дифференцируемы для x>a ,

, то

,

если последний существует, конечный или бесконечный.

Доказательство . Сделаем замену

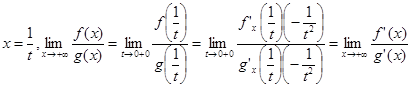
Замечание. Аналогичные утверждения имеют место для x ® - ¥.

3.2 Раскрытие неопределенностей вида ¥/¥