Курсовая работа: Распределение Пуассона Аксиомы простейшего потока событий
Для симметричных случайных величин, у которых плотности
распределения симметричны относительно некоторой точки![]() , нижние и верхние критические границы удовлетворяют условию
, нижние и верхние критические границы удовлетворяют условию ![]() , что дает возможность приводить таблицы лишь для процентных точек или квантилей, больших
, что дает возможность приводить таблицы лишь для процентных точек или квантилей, больших ![]() . Так, для стандартной нормальной случайной величины с уровнем значимости
. Так, для стандартной нормальной случайной величины с уровнем значимости ![]()
![]() .
.
Квантиль, односторонние и двухсторонние критические границы изображены на рис.1.

Рис.1. р-квантиль и критические точки для закона распределения ![]() .
.
1.1.1 Доверительная оценка при неизвестной вероятности по большим выборкам
Частота ![]() является точечной оценкой
является точечной оценкой ![]() , она асимптотически нормально распределена с
, она асимптотически нормально распределена с ![]() и
и 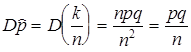 .
.
Если ![]() ,то
,то ![]() . Зададим
. Зададим ![]() . Величина
. Величина ![]() такая, что
такая, что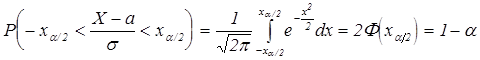 может быть найдена из уравнения
может быть найдена из уравнения ![]() при помощи таблиц для функций Лапласа. Эти же рассуждения применим к
при помощи таблиц для функций Лапласа. Эти же рассуждения применим к ![]() . По заданному
. По заданному ![]() можно найти
можно найти ![]() так, чтобы
так, чтобы 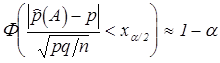 . Из неравенства
. Из неравенства 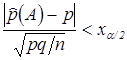 следует, что
следует, что 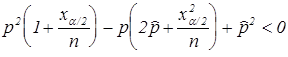 , откуда можно вычислить оба значения
, откуда можно вычислить оба значения ![]() и
и ![]() , которые представляют доверительные оценки для
, которые представляют доверительные оценки для ![]() . Если
. Если ![]() выбрано достаточно малым, то случайный интервал
выбрано достаточно малым, то случайный интервал ![]() “покрывает”
“покрывает” ![]() почти наверное.
почти наверное.
1.1.2 Доверительные оценки для параметров нормального закона
1.1.2.1 Доверительная оценка ![]() при известном
при известном ![]()
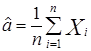 ,
,![]() , тогда
, тогда 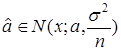 .
.
Соответственно,
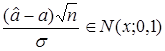 .
.
Для стандартной нормальной случайной величины с уровнем значимости ![]() нижняя и верхняя критические границы соответственно равны
нижняя и верхняя критические границы соответственно равны ![]() и
и ![]() .
.
Имеем
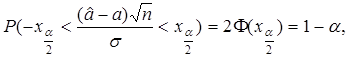 или
или
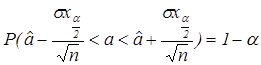 .
.
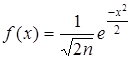 .
.
Таким образом, 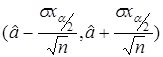 - доверительная оценка для параметра a с мерой надежности
- доверительная оценка для параметра a с мерой надежности ![]() .
.
1.1.2.2 Доверительная оценка ![]() при неизвестном
при неизвестном ![]()
Оценка основана на том факте, что при высказанных предположениях величина ![]() удовлетворяет t- распределению с n-1 степенями свободы.
удовлетворяет t- распределению с n-1 степенями свободы.
Определяя одностороннюю критическую точку ![]() из условия
из условия 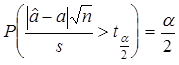 ,получим доверительную оценку для а в виде
,получим доверительную оценку для а в виде
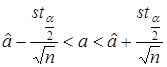 .
.
Для конкретной выборки ![]() объема n доверительная оценки для а становится ее доверительным интервалом.
объема n доверительная оценки для а становится ее доверительным интервалом.
1.1.2.3 Доверительная оценка![]() при неизвестном
при неизвестном ![]()
Отправной точкой является тот факт, что при заданных предпосылках величина ![]() удовлетворяет
удовлетворяет ![]() - распределению с n-1 степенями свободы. По заданному уровню значимости
- распределению с n-1 степенями свободы. По заданному уровню значимости ![]() и
и ![]() степенями свободы находим критические точки
степенями свободы находим критические точки ![]() и
и ![]() распределения
распределения ![]() такие, что
такие, что
![]() ,
, ![]()
![]() , или
, или 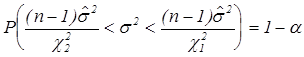 .
.
Таким образом , 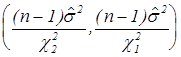 есть доверительная оценка
есть доверительная оценка ![]() с мерой надежности
с мерой надежности ![]() .
.
1.2 Метод наибольшего правдоподобия