Курсовая работа: Распределение Пуассона Аксиомы простейшего потока событий

Как уже отмечалось , в математической статисти­ке существуют два вида оценок: точечные и интервальные. В этой главе будут рассмотрены точечные оценки, а интерваль­ным оценкам посвящена следующая глава.

1.3.1. Состоятельные, несмещенные и эффективные оценки

Пусть— случайная выборка из генеральной совокупности X, функция распределениякоторой известна, а— неизвестный параметр, т.е. рассматривается параметрическая модель(для простоты изложения будем считать пока, что— скаляр).

Требуется построить статистику, которую можно было бы принять в качестве точечной оценки параметра.

Интуитивно ясно, что в качестве оценки параметрамож­но использовать различные статистики. Например, в качестве точечной оценки дляможно предложить такие статистики:

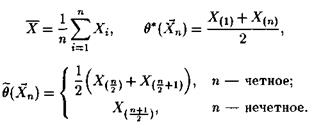
Какую же из этих статистик предпочесть? В общем случае нужно дать ответ на вопрос: какими свойствами должна обла­дать статистика, чтобы она была в неко­тором смысле наилучшей оценкой параметра в? Рассмотрению требований к оценкам и методам их нахождения посвящена на­стоящая глава.

Заметим, что в дальнейшем, как правило, будем говорить об оценке параметрапараметрической модели, хотя все ска­занное можно перенести и на функцию от в.

Определение 1.3.1.1 Статистикуназывают состоятельной оценкой параметра, если с ростом объема выборки п она сходится по вероятности к оцениваемому пара­метру , т.е.

Иными словами, для состоятельной оценкиотклонение ее отна величину е и более становится маловероятным при большом объеме выборки. Это свойство оценки является очень важным, ибо несостоятельная оценка практически беспо­лезна. Однако следует отметить, что на практике приходится оценивать неизвестные параметры и при малых объемах вы­борки.

Естественным является то требование, при выполнении ко­торого оценка не дает систематической погрешности в сторону завышения (или занижения) истинного значения параметра.

Определение 1.3.1.2. Статистикуназывают несмещенной оценкой параметра, если ее математическое ожи­дание совпадает с, т.е.для любого фиксирован­_испер.

Если оценка является смещенной (т.е. последнее равенство не имеет места), то величина смещения Как мы увидим далее, смещение оценки часто можно устра­нить, введя соответствующую поправку.

Говорят также, что оценкаявляется асимптотически несмещенной, если приона сходится по вероятности к своему математическому ожиданию, т.е. для любого

Предположим, что имеются две несмещенные оценки и для параметра. Если дисперсииудовлетворяют условию

(1.3.1)

для любого фиксированного пи, то следует предпочесть оценку, поскольку разброс статистики относительно параметраменьше, чем разброс статистики

Определение 1.3.1.3. Если в некотором классе несмещенных оценок параметра, имеющих конечную дисперсию, существу­ет такая оценка, что неравенство (2.1) выполняется для всех оценокиз этого класса, то говорят, что оценка является эффективной в данном классе оценок.

оценивать неизвестные параметры и при малых объемах вы­борки.

Естественным является то требование, при выполнении ко­торого оценка не дает систематической погрешности в сторону завышения (или занижения) истинного значения параметра.

Определение 1.3.1.4. Статистикуназывают несмещенной оценкой параметра, если ее математическое ожи­дание совпадает с, т.е.для любого фиксирован­н_испер

Если оценка является смещенной (т.е. последнее равенство не имеет места), то величина смещения Как мы увидим далее, смещение оценки часто можно устра­нить, введя соответствующую поправку.

Говорят также, что оценкаявляется асимптотически несмещенной, если приона сходится по вероятности к своему математическому ожиданию, т.е. для любого

Предположим, что имеются две несмещенные оценки и для параметра. Если ди_исперсии

удовлетворяют условию

(1.3.2)

для любого фиксированного пи, то следует предпочесть оценку, поскольку разброс статистикиотносительно параметраменьше, чем разброс статистики