Курсова робота: Рішення лінійних рівнянь першого порядку

Зміст

1. Введення

2. Постановка задачі

3. Знаходження власних чисел і побудова ФСР

4. Побудова фундаментальної матриці рішень методом Ейлера

5. Знаходження наближеного рішення у вигляді матричного ряду

6. Побудова загального рішення матричним методом

7. Задача Коші для матричного методу

8. Рішення неоднорідної системи

Графіки

Висновок

Література

1. Введення

Розглянемо систему лінійних рівнянь першого порядку, записану в нормальній формі:

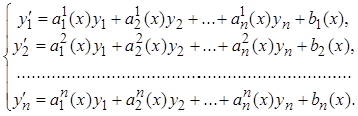(1)

де коефіцієнти а_ij, i=1,2,….,n, до=1,2,.,n, є постійними величинами;

y_i =y_i (t), i=1,2,…,n-невідомі функції змінної t.

Якщо всі b_i (t) (i=1,2,…,n) покласти рівним нулю (b_i (t) =0), те вийде однорідна система, що відповідає неоднорідній системі (1).

Позначаючи матрицю системи через А (х), а вектор через тоді систему (1) можемо переписати в матричній формі

(1а)

Якщо , то одержуємо відповідну систему однорідних рівнянь

. (2)

Усяка сукупність n функцій

певних і безупинно в інтервалі (a; b), називається рішенням системи (1) у цьому інтервалі, якщо вона обертає всі рівняння системи (1) у тотожності:

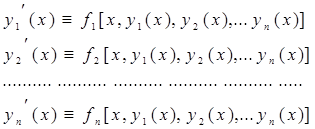
справедливі при всіх значеннях x з інтервалу (a, b). Загальне рішення неоднорідної системи являє собою суму загального рішення відповідної однорідної системи й приватного рішення неоднорідної.

2. Постановка задачі

Ціль роботи: дослідження методів рішення системи диференціальних рівнянь із постійною матрицею:

; ;

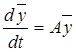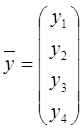
--> ЧИТАТЬ ПОЛНОСТЬЮ <--