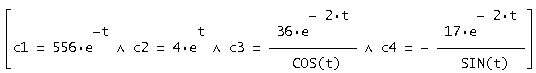3. При наявності серед корінь характеристичного полінома корінь комплексно-комплексно-сполучених Жорданова клітка виглядає в такий спосіб:

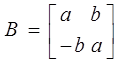
де а комплексно сполучений корінь характеристичного полінома.

Тому що в нашім випадку серед характеристичних чисел присутні, як комплексно-комплексно-сполучені корінь л = 2 - ?? л = 2 +?, так і дійсний різних корінь л = - 1? л = 1, те жорданова матриця виглядає в такий спосіб:

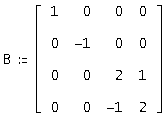
З рівняння A_* S = S_* В, де S - матриця, одержуємо систему 16-го порядку, з якої знаходимо елементи матриці S. Отримана матриця S буде виглядати в такий спосіб:

Вирішуємо систему 16-го порядку з рівняння A_* S = S_* В

Знаходимо деякі елементи й одержуємо наступну матрицю S:

Зробимо перевірку A_* S - S_* В=0:

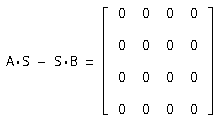
Значить матриця переходу знайдена вірно.

Для знаходження вектора рішень y необхідно помножити матрицю S на , де - це вектор, елементи якого залежать від корінь характеристичного багаточлена:

Для комплексних чисел має такий вигляд:

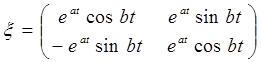
Для випадку корінь дійсних різних:

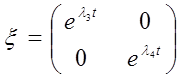
У нашім випадку виходить рівної:

=

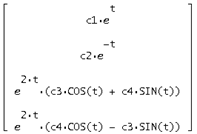
Звідси знайдемо загальне рішення в=S*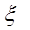, одержимо:

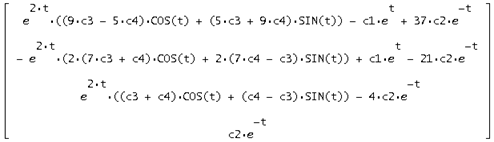
При підстановці рішення у вихідну систему виходить вірна рівність, із цього треба, що рішення знайдене вірно:

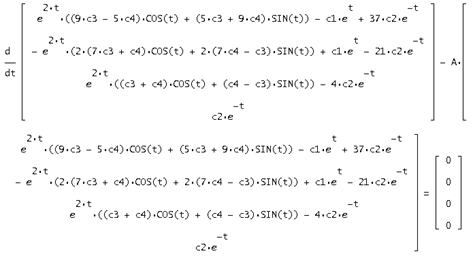
7. Задача Коші для матричного методу

Необхідно із всіх рішень системи рівнянь знайти таке рішення, у якому y ^{(i) (} t) приймає задане числове значення y_0i у заданій крапці, тобто знайти значення с_i для наступних заданих значень: x=0, y= [1, 2, 3,4].

У вектор рішень y (t) підставляємо задані умови й вирішуємо отриману систему відносно c1, c2, c3, c4:

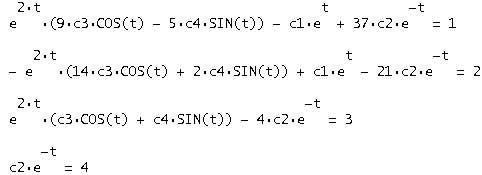
У результаті одержуємо: