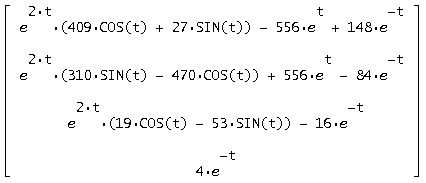
Зробимо перевірку, підставивши загальне рішення у вихідну систему

:

Вийшов нульовий вектор . Отже, знайдена матриця є рішенням вихідної системи.

Дослідження залежності жордановой форми матриці А від властивостей матриці системи.

Нехай J - жорданова клітка матриці А. Для випадку дійсних різних корінь жорданова клітка буде виглядати в такий спосіб:

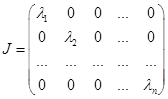
Нехай серед дійсних власних чисел матриці А є кратні. Жорданова клітка буде перебувати по наступній формулі:

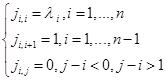
Наприклад, якщо кратність k=2, те жорданову клітку матриці ми можемо записати так:

Якщо кратність k=3, то жорданову клітку матриці ми можемо записати так:

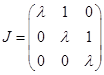
Якщо ж серед трьох власних чисел є коріннями кратності 2, то жорданова форма буде виглядати в такий спосіб:

Якщо два власних числа матриці А є комплексними сполученими, то запис жордановой клітки буде виглядати так:

де - дійсна, - мнима частина власного числа .

8. Рішення неоднорідної системи

Права частина:

Загальне рішення неоднорідної системи можна знайти по формулі:

Де - фср, З - матриця , F (t) - вектор праві частини.

- загальне рішення однорідної системи

- приватне рішення неоднорідної системи

Отримане приватне рішення неоднорідної системи:

Загальне рішення однорідної системи