Курсовая работа: Рішення лінійних рівнянь першого порядку
1. Знайти власні числа й побудувати фундаментальну систему рішень (ФСР).
2. Побудувати фундаментальну матрицю методом Ейлера.
3. Знайти наближене рішення у вигляді матричного ряду.
4. Побудувати загальне рішення матричним методом. Досліджувати залежність Жорданової форми матриці А від її власних чисел.
5. Вирішити задачу Коші.
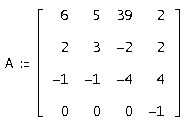
Початкові умови:
Вектор початкових умов: [1, 2, 3, 4]
t = 0
3. Знаходження власних чисел і побудова ФСР
Однорідною лінійною системою диференціальних рівнянь називається система рівнянь виду:
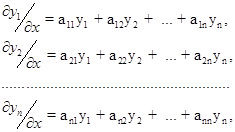 (3)
(3)
Якщо в матриці системи ![]() всі
всі ![]() =const, то дана система називається системою з постійними коефіцієнтами або з постійною матрицею.
=const, то дана система називається системою з постійними коефіцієнтами або з постійною матрицею.
Фундаментальною системою рішень однорідної лінійної системи рівнянь називається базис лінійного простору рішень (, тобто n лінійно незалежних рішень цієї системи.
Для побудови фундаментальної системи рішень диференціального рівняння необхідно знайти власні числа характеристичного полінома, тому що залежно від їхнього виду (характеристичні числа можуть бути дійсними різними, кратними, комплексними) будується фундаментальна система рішень. Для того щоб ця система n лінійних однорідних рівнянь із n невідомими мала нетривіальне рішення, необхідно й досить, щоб визначник системи (вронскиан) дорівнює нулю:
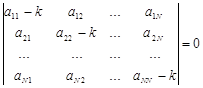 (4)
(4)
Із цього рівняння ступеня n визначається значення k, при яких система має нетривіальні рішення. Рівняння (4) називається характеристичним.
Запишемо характеристичний поліном, для цього скористаємося функцією CHARPOLY

![]()
Для знаходження власних чисел скористаємося функцією SOLVE (U, (), що повертає характеристичні числа матриці А в вектор (. Одержимо:
![]()
![]()
Вийшло два дійсно корені ![]() й два комплексно-комплексно-сполучених корені
й два комплексно-комплексно-сполучених корені ![]() . Отже, вектора, що утворять фундаментальну матрицю, для даного типу корінь будуть перебувати окремо для
. Отже, вектора, що утворять фундаментальну матрицю, для даного типу корінь будуть перебувати окремо для ![]() й окремо для
й окремо для ![]() . Запишемо ФСР для даних для отриманих характеристичних чисел:
. Запишемо ФСР для даних для отриманих характеристичних чисел:
Матрицю y (x (, стовпцями якої є рішення, що утворять фундаментальну систему, називають фундаментальною матрицею.

І загальне рішення системи буде виглядати в такий спосіб:
![]()

Знайдемо рішення даної системи за допомогою методу Ейлера.
4. Побудова фундаментальної матриці рішень методом Ейлера
Метод Ейлера полягає в наступному.