Приблизно вектор рішень можна знайти як добуток матричного ряду:

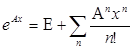
і вектора початкових умов y₀ = [y₁ ,y₂ , ….y_k ].

Формула є матричною задачею Коші в наближеному виді.

Експонентою матриці А називається сума ряду

де Е - одинична матриця. Матриця є рішенням матричної задачі Коші: є фундаментальною матрицею системи. Знайдемо розкладання матричного ряду послідовно по сімох, вісьмох і десяти перших членах.

Для одержання розкладання по 7 перших членах (аналогічно по 8,10 і 10). Результатом буде матриця 4*4. Отримані матриці множимо на вектор початкових умов S= [1,2,3,4] і одержуємо наближене рішення у вигляді матричного ряду.

При збільшенні членів розкладання ряду вектор наближених рішень буде прагнути до вектора точних рішень. Цей факт можна спостерігати, графічно порівнюючи зображення точного й наближеного рішень (див. додаток).

Помножимо на відповідний вектор початкових умов і одержимо наближене рішення у вигляді матричного ряду, запишемо отримане рішення для n=7.

[s1 ≔ 1, s2 ≔ 2, s3 ≔ 3, s4 ≔ 4]

6. Побудова загального рішення матричним методом

Матричний метод рішення системи рівнянь (1) заснований на безпосереднім відшуканні фундаментальної матриці цієї системи.

??????????? e^A ??????? ? ??????????? ???? ????

де Е - одинична матриця.

Властивість матричної експоненти: а) якщо АВ=ВА, те е^А+В =е^А *е^В = е^В *е^А ; б) якщо А=S^- 1*B*S, те е^А =S^-1 *e^B *S, де матриця S - це матриця перетворення змінних із власного базису в базис вихідних змінних. в) матриця y (t) =e^At є рішенням матричної задачі Коші: т.е. є фундаментальною матрицею системи (1).

Із властивості в) треба, що рішення y (t) системи (1) задовольняючій умові y (0) =y₀ , визначається вираженням y (t) =e^At *y₀ . Таким чином, задача знаходження рішень системи рівнянь (1) еквівалентна задачі відшукання матриці e^At по матриці А.

Для обчислення матриці e^At зручно представити матрицю А в виді:

,

де матриця S - це матриця перетворення змінних із власного базису в базис вихідних змінних, а B_А - жорданова форма матриці А, тому що e^At = S^-1 *e^Bt *S.

Жорданова форма матриці залежить від виду характеристичних чисел.

1. Нехай характеристичні числа дійсні кратні, тоді Жорданова форма матриці розмірності nxn має вигляд:

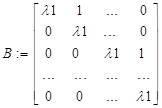
де - дійсний корінь кратності n.

2. Якщо серед корінь характеристичного полінома є, як дійсні різні, так і дійсних кратних корінь, то матриця В має вигляд: