Курсовая работа: Розрахунок типових задач з математичної статистики

Значення функції Лапласа затабульовані, або ж їх можна підрахувати за допомогою математичних пакетів прикладних програм. Хоча з досить високою точністю можна й самому підрахувати значення функції Лапласа, використавши наступну наближену формулу (підінтегральну функцію було розкладено в ряд та взято інтеграл):

.

Функція розподілення імовірності нормального розподілення пов’язана з функцією Лапласа наступним співвідношенням:

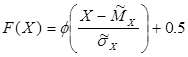, якщо X>0,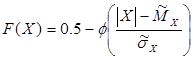, якщо X<0.

Знову перейдемо в обчисленнях від загальної до центрованої нормальної величини:

.

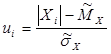Це зафіксовано у п’ятій строчці Таблиці 4.2. Тоді імовірність попадання випадкової величини X в інтервал (X_i ; X_i+1 ) можна виразити через функцію Лапласа так:

,

де значення - нормована нормальна випадкова величина, що відповідає X_i (результат занесено в шосту строчку Таблиці 4.2). Знаючи теоретичну імовірність P_i ⁰ , можна буде обчислити теоретичну кількість n_i ⁰ попадань випадкової величини X в і-й інтервал (X_i ; X_i+1 ) з Таблиці 4.2 (і результат занесено у відповідну сьому строчку Таблиці 4.2).

Таблиця 4.1 Інтервали розбиття

1	2	3	4	5	6	7	8	9	10	11
(-5; - 4)	(-4; - 3)	(-3; - 2)	(-2; - 1)	(-1; 0)	(0; 1)	(1; 2)	(2; 3)	(3; 4)	(4; 5)	(5; 6)
1	2	1	14	18	22	25	15	1	0	1
0.01	0.02	0.01	0.14	0.18	0.22	0.25	0.15	0.01	0	0.01

Таблиця 4.2 Розраховані імовірності

I	1	2	3	4	5
(Xi ; Xi+1 )	(-5; - 1)	(-1; 0)	(0; 1)	(1; 2)	(2; 6)
ni	18	18	22	25	17
	0.18	0.18	0.22	0.25	0.17
(ui ; ui+1 )	(2.8395; 0.2969)	(0.2969; 0)	(0; 0.2969)	(0.2969; 0.9322)	(0.9322; 3.4752)
Pi 0	0.3798	0.1179	0.1179	0.2059	0.1760
ni 0	38	12	12	21	18