Курсовая работа: Розрахунок типових задач з математичної статистики
Будуємо за даними Таблиці 4.1 гістограму (рис.4.1) - експериментальний варіант графіка функції щільності імовірності. Будуємо гістограму, бо маємо справу з попаданням безперервної випадкової величини X в один з інтервалів розбиття на рівновіддалені.
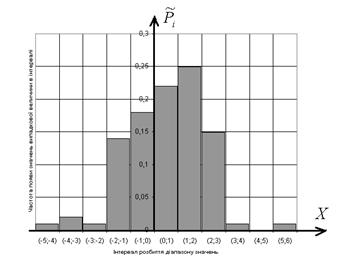
Рис.4.1 Гістограма експериментального графіку функції щільності імовірності.
Аналізуємо обчислені оцінки математичного чекання та отриману гістограму.
Безперервна випадкова величина X приймає від’ємні значення. Отже, їй залишається бути розподіленою за нормальним (гаусовським) законом розподілення.
„Правило 3-х сігм” приблизно виконується (більшість значень дійсно лежить в інтервалі (-4.165276; 5.252514)). Відхилення практичної гістограми від теоретичної допоможе оцінити характеристика асиметрії та ексцес.
Таким чином, висуваємо гіпотезу H0 - випадкова величина X розподілена за нормальним законом розподілення.
Для обчислення теоретичних частот попадання випадкової величини X в коректований інтервал (з Таблиці 4.2) можна використовувати дві методики. Ми будемо застосовувати другу як більш теоретично обґрунтовану та правильнішу, а також точнішу.
Перша методика проста, але обчислення на її основі носять приблизний, оціночний характер. Перейдемо в обчисленнях від загальної до центрованої нормальної величини. Теоретично наша випадкова величина вважається розподіленою за загальним нормальним законом. Його функція щільності імовірності має в нашому випадку вигляд:
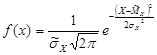 .
.
Перехід до центрованої нормальної величини:
![]() .
.
Функція щільності імовірності для неї:
![]() .
.
Таким чином
![]() .
.
Імовірність попадання випадкової величини X в інтервал (Xi ; Xi+1 ) дорівнює
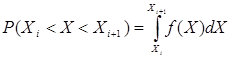 .
.
Дорівнює площі фігури, обмеженої графіком щільності імовірності, віссю 0X та прямими X=Xi , X=Xi+1 .
Тобто можна приблизно вважати ії рівною добутку довжини інтервалу h на значення функції щільності імовірності в середині інтервалу (вищесказане є фактично двосторонньою оцінкою визначеного інтегралу):
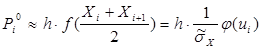 ,
,
де значення ![]() відповідає середині інтервалу
відповідає середині інтервалу
![]() .
.
Знаючи теоретичну імовірність Pi , можна буде обчислити теоретичну кількість ni попадань випадкової величини X в і-й інтервал (Xi ; Xi+1 ).
Але це буде дуже приблизна оцінка, бо коректування інтервалів розширило межі інтервалів та збільшило різницю між значеннями функції щільності імовірності в них. Точність цього методу обчислення теоретичних частот буде зростати при зменшенні інтервалу розбиття. Проте, це не можливо без порушення правила розбиття діапазону зміни значень випадкової величини в методі Пірсона. З загальних теоретичних відомостей імовірність попадання випадкової величини X в інтервал (Xi ; Xi+1 ) можна виразити через функцію щільності імовірності
![]() ,
,
або через функцію розподілення імовірності
![]()
![]() .
.
Для нормованого нормального розподілення функція розподілення імовірності обчислюється через функцію Лапласа (сама функція Лапласа не є функцією розподілення імовірності):