Курсовая работа: Синтез следящей системы с обратной связью по току и по скорости

. (10)

В случае отсутствия последовательного корректирующего устройства (при П(р)=1) обратная передаточная функция для системы с обратной связью по току определится следующим образом:

. (11)

2. Постановка задачи синтеза

В том случае, если в качестве исходных данных заданы принципиальная схема системы и параметры ее основных элементов, а также требования к динамическим свойствам, постановка задачи может быть сформулирована следующим образом: с целью улучшения показателей качества управления в определенные места системы включаются устройства, называемые корректирующими.

Корректирующие устройства бывают последовательные и параллельные.

В качестве основного метода синтеза в курсовом проекте применяется метод обратных логарифмических частотных характеристик.

Сущность этого метода сводится к следующему. Пусть задана структурная схема следящей системы в самом общем виде, содержащая последовательное П(р) и параллельное К(р) корректирующие устройства и охваченную часть системы W₀ (p) (см. рис.3).

Рис.3.

В процессе синтеза надо стараться ввести такие корректирующие устройства, которые изменят исходную ЛАЧХ системы таким образом, чтобы ЛАЧХ скорректированной системы совпадала с желаемой ЛАЧХ. Тогда передаточная функция разомкнутой скорректированной системы:

,

а соответствующая ей обратная передаточная функция:

.

Обеспечение требуемых динамических свойств, определяемых быстродействием, ошибкой, запасами устойчивости, достигается путем введения в структурную схему системы параллельных корректирующих устройств, которые деформируют ОЛАЧХ исходной системы в существенном диапазоне частот (см. рис.4).

Последовательные корректирующие устройства обладают повышенной чувствительностью к помехам и ухудшают динамику системы при изменении ее параметров.

Замечаем, что в диапазоне частот

,

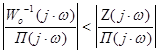а следовательно

.

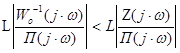Ввиду этого, можно приближенно считать, что в рассматриваемом диапазоне частот ЛАЧХ синтезированной системы определяется ЛАЧХ параллельного корректирующего устройства (так как обе части делятся на одно и то же число):

.

С другой стороны, в диапазоне частот и

.

Поэтому

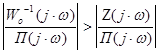
и, следовательно, в рассматриваемых диапазонах справедливо равенство

.

Поэтому ОЛЧХ скорректированной системы приближенно можно представить в виде ломаной ABCDEF, как это показано на рис.4. Здесь ОЛЧХ синтезированной САР состоит из тех участков, определяемых охваченной частью 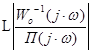(участки AB иDEF), и прямой ЛАЧХ, определяемой параллельным корректирующим устройством (участок BCD), которые оказываются большими по своей ординате.