Курсовая работа: Сравнительный анализ численных методов

Рисунок 12. Решение системы уравнений методом простых итераций

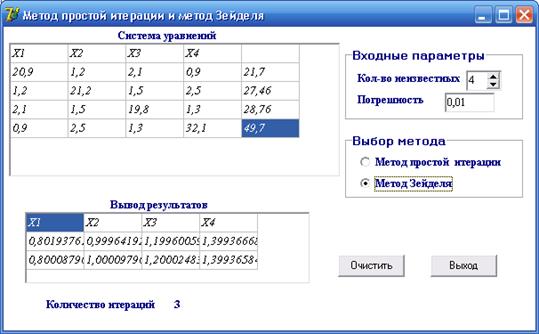
Рисунок 13. Решение уравнения методом Зейделя

Раздел 4. Сравнительный анализ методов численного дифференцирования и интегрирования

4.1 Методы численного дифференцирования

Необходимость численного дифференцирования может возникнуть при необходимости исследований функций заданных табличным образом, кроме тех случаев, когда вычисление производной численно может оказаться проще, чем дифференцирование.

Предположим, что в окрестности точки xi функция F(x)дифференцируема достаточное число раз. Исходя из определения производной:

используем для её вычисления две приближенные формулы:

(1)

(2)

Формулы (1) и (2) называют правыми и левыми разностными производными.

Для оценки погрешностей формул численного дифференцирования используется формула Тейлора:

откуда можно вычислить:

(3)

Выражение (3) имеет погрешность порядка (x-xi), следовательно, формулы правых и левых разностных производных имеют погрешность одного порядка с h , где

h=xi-xi-1

Такая точность достаточно невысока, поэтому применяется так называемая центрально-симметричная форма производной, погрешность которой одного порядка с h2

(4)

Хотя очевидно, что формула (4) используется для внутренних точек отрезка.

Для примера возьмём ряд точек:

Вычислим производную функции f(x)=sin(x) в одной из них двумя способами.

Очевидно, что h=

По центрально-симметричной формуле:

По формуле левой разностной производной: