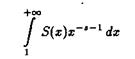Курсовая работа: Теорема Дирихле

А(c)=

а q(t) – комплекснозначная функция, непрерывно дифференцируемая на множестве 1£t£¥

Тогда

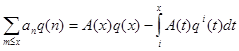(2.2)

Если же

то

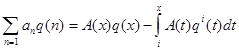(2.3)

при условии, что ряд в левой части равенства сходится.

Доказательство. Положим А(0)=0 и В(х) равным левой части равенства (2.2). Тогда при любом натуральном N

так как А(0)=0. Далее

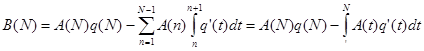
поскольку функция А(х) постоянна на каждом полуинтервале n£t<n+1. Следовательно, равенство (2.2) доказано при целых значениях х.

пусть х³1 – произвольное число. Положим N=[x]; значит, N£x£N+1. Тогда А(х)=А(N), B(x)=B(N), а

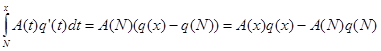
Следовательно,

Тем самым доказано, что равенство (2.2) верно и для нецелых чисел значений х.

Равенство (2.3) получаем из равенства (2.2) переходом к пределу при х®¥. Лемма доказана.

Воспользовавшись леммой 4, получим следующее равенство

(2.4)

где

функция, введенная Лемме 4.

Для s = p+it из области ReS = s, где s – некоторое положительное число, пользуясь леммой 4, находим

Поэтому интеграл