Курсовая работа: Уравнение и функция Бесселя
.
Следовательно,
. (10)
Таким образом, операция 
(состоящая в дифференцировании с последующим умножением на 
), примененная к 
, повышает в этом выражении индекс 
на единицу и меняет знак. Применяя эту операцию 
раз, где – любое натуральное число, получаем:
. (10`)
Имеем:
;
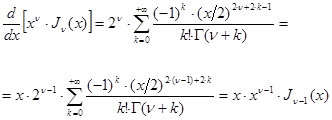
Следовательно,
. (11)
Таким образом, операция , примененная к 
, понижает в этом выражении индекс 
на единицу. Применяя эту операцию раз, получаем:
. (11`)
Из выведенных формул можно получить некоторые следствия. Используя (10), получим:
; 
; 
.
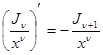Отсюда, в частности, следует, что 
. Используя (11), получим:
; 
; 
.
Почленное сложение и вычитание полученных равенств дает:
, (12)
. (13)
Формула (13) позволяет выразить все бесселевы функции с целыми индексами через 
, 
. Действительно, из (13) находим (полагая 
):
, (13`)
откуда последовательно получаем:
,
, …………………
3. Бесселевы функции с полуцелым индексом
Бесселевы функции, вообще говоря, являются новыми трансцендентными функциями, не выражающимися через элементарные функции. Исключение составляют бесселевы функции с индексом 
, где 
– целое. Эти функции могут быть выражены через элементарные функции.
Имеем:
,
,
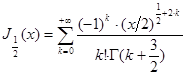следовательно,