Курсовая работа: Уравнение и функция Бесселя

откуда видно, что если и являются разными нулями функции , то

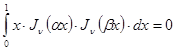. (23`)

Этим доказано, что при система функций

на интервале является ортогональной относительно веса .

Переходя к пределу при в соотношении

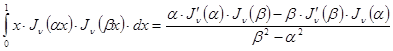
и используя правило Лопиталя, получим при всяком

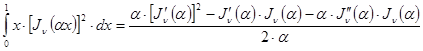, (24)

следовательно, если является нулем функции , то

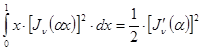. (24`)

Таким образом, при каждом всякой непрерывной функции на , удовлетворяющей требованию

,

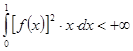поставлен в соответствие ряд Фурье-Бесселя

, (25)

коэффициенты которого определяются формулами

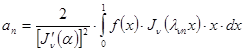. (25`)

Можно доказать, что система функций на , ортогональная относительно веса , замкнутая. В частности, если ряд Фурье-Бесселя (25) равномерно сходится к порождающей его непрерывной функции .

Можно показать, что если и непрерывная на и кусочно-гладкая на функция, то ряд Фурье-Бесселя этой функции сходится к ней при .

6. Асимптотическое представление бесселевых функций с целым индексом для больших значений аргумента

Пусть - положительная функция и - какая-нибудь (вообще комплекснозначная) функция, определенные для достаточно больших значений . Запись

при

означает, что найдутся такие числа и M, что при имеем .

Подобная запись употребляется и в других аналогичных случаях. Например, если - положительная функция и - какая-нибудь функция, определенные для достаточно малых положительных значений , то запись

при

означает, что найдутся такие числа и , что на .

Вспомогательная лемма

Если дважды непрерывно дифференцируема на , то для функции

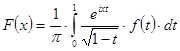
имеет место асимптотическое представление