Курсовая работа: Уравнение и функция Бесселя

,

найдем, что система коэффициентов этого ряда будет искомой системой .

Формулы для коэффициентов ряда Лорана позволяют выразить функции рассматриваемой системы через производящую функцию. Применяя эти формулы и преобразовывая затем интеграл вдоль единичной окружности в простой интеграл, получим:

. (17)

Производящая функция системы бесселевых функций с целыми индексами

Покажем, что для системы бесселевых функций первого рода с целыми индексами (…) производящая функция есть:

.

Имеем:

, ,

откуда после почленного перемножения этих равенств найдем:

(так как в предпоследней внутренней сумме и были связаны зависимостью , то мы могли положить , получив суммирование по одному индексу ). В последней внутренней сумме суммирование производится по всем целым , для которых , следовательно, при это будет ; при это будет . Таким образом, во всех случаях внутренняя сумма есть в силу формул (5`) и (5```). Итак,

, (18)

но это и доказывает, что есть производящая функция для системы .

Выведем некоторые следствия из формулы (18). Полагая в ней , получим:

,

откуда после разделения действительной и мнимой части (учитывая, что )

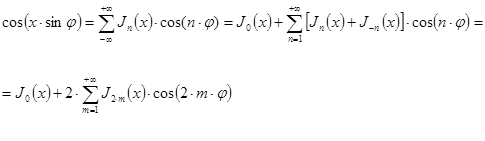(18`)

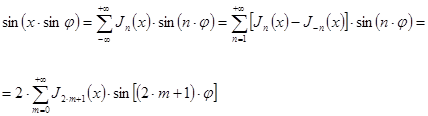(18``)

Заменяя в (18`) и (18``) на , найдем:

, (18```)

. (18````)

Интегральное представление J_n (x)

Так как, по доказанному, при имеем , то по формуле (17) получаем (используя в преобразованиях формулы Эйлера):

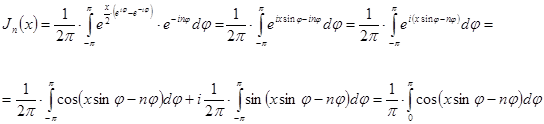
где принято во внимание, что есть четная функция от есть нечетная функция от . Итак, доказано, что для любого целого числа

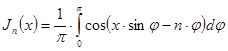. (19)

Формула (19) дает представление бесселевых функций с целым индексом в виде определенного интеграла, зависящего от параметра . Эта формула называется интегральным представлением Бесселя для , правая часть формулы называется интегралом Бесселя. В частности, при найдем:

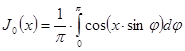. (19`)

5. Ряды Фурье-Бесселя