Курсовая работа: Уравнение и функция Бесселя

, , (20)

где и – непрерывные функции на . Пусть и – ненулевые решения этих уравнений. Умножение на и на и последующее вычитание дают

.

Пусть и принадлежат и , тогда после интегрирования в пределах от до получим

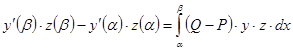. (21)

Если и – соседние нули решения , то между и сохраняет постоянный знак, пусть, например, на (, ) (в противном случае следует заменить на ), тогда , (равенство нулю исключено, так как – ненулевое решение дифференциального уравнения второго порядка). Если на , то должна, по крайней мере, раз обращаться в нуль между и , так как иначе сохранит постоянный знак на (,). Пусть, например, на (,) (в противном случае заменяем на ), и тогда из (21) получим противоречие, ибо левая часть ≤0, а правая >0. Таким образом доказана теорема сравнения Штурма: если P(x)<Q(x) на рассматриваемом интервале I и если y и z – ненулевые решения уравнений (20), то между каждыми двумя соседними нулями y(x) находится по крайней мере один нуль z(x).

Из теоремы сравнения Штурма вытекают нижеследующие следствия. Если на , то каждое ненулевое решение уравнения может иметь на не более одного нуля (это легко видеть, если положить и взять ). Если на (где ), то для всяких двух соседних нулей и () каждого ненулевого решения уравнения имеем (это легко видеть, если положить , взять и заметить, что нулями будут только числа вида , целое). Если на (где ), то для всяких двух соседних нулей каждого ненулевого решения уравнения имеем (это легко видеть, если положить и взять ). Из сказанного следует, что если на , то для всяких двух соседних нулей и () каждого ненулевого решения уравнения имеем .

Изложенное показывает, что если непрерывна на и превышает некоторое положительное число вблизи +∞, то каждое ненулевое решение уравнения имеет на бесконечно много нулей. Если еще вблизи не обращается в нуль, то эти нули образуют бесконечную возрастающую последовательность , имеющую пределом +∞, а если, кроме того, , где , то .

Рассмотрим уравнение Бесселя

на интервале . Подстановка приводит к уравнению

.

Очевидно, и имеют одни и те же нули. Так как , где – целая функция, то не имеет нулей на при достаточно малом , и так как при , то при каждом нули на образуют бесконечную возрастающую последовательность

причем .

Если , то удовлетворит уравнению

на интервале (0, +∞). Подстановка приводит к уравнению

и, следовательно, удовлетворяет этому уравнению. Таким образом, при любых положительных и имеем

, где ,

, где ,

откуда

,

следовательно,

, где . (22)

Пусть теперь . Разложение по степеням начинается с члена, содержащего , разложение по степеням начинается с члена, содержащего , так как коэффициент при равен нулю, что легко видеть, исходя из формулы (5). Следовательно, из (22) при получим

,

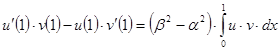то есть