Курсовая работа: Уравнение и функция Бесселя

Докажем эту лемму. Заменяя на , получим:

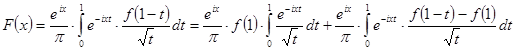. (26)

Рассмотрим интеграл, фигурирующий в первом слагаемом правой части формулы (20). Заменяя на , найдем:

,

но, заменив на , получим:

.

Если положительна, убывает и стремиться к нулю при , то и , а следовательно, и есть при , поэтому

при ,

откуда

при .

Итак, получаем асимптотическое представление:

при . (27)

Рассмотрим теперь интеграл, фигурирующий во втором слагаемом правой части формулы (20). Имеем:

,

.

Очевидно, дважды непрерывно дифференцируема на , но существуют и , поэтому становится непрерывно дифференцируема на . Интегрирование по частям дает:

,

где первое слагаемое правой части есть при , а интеграл во втором слагаемом несобственный при нижнем пределе мажорируется интегралом

,

который сходится, так как

при ;

следовательно, второе слагаемое есть тоже при .

Итак, имеем:

при . (28)

Из (26), (27), (28) получаем искомое асимптотическое представление:

при . (29)

Из этой формулы, переходя к сопряженным величинам, найдем еще:

при . (29`)

Формулы (29) и (29`) верны и для комплекснозначных функций .