Курсовая работа: Вариации при исчислении

Будем считать, что функция u(х) непрерывна и имеет непрерывные производные до второго порядка включительно.

Уравнение Эйлера для функционала (28) будет иметь вид

(1.29)

Таким образом, получили краевую задачу для линейного дифференциального уравнения второго порядка с постоянными коэффициентами. Общее решение уравнения (1.29) будет иметь вид

.

Для нахождения произвольных постоянных с₁ и с₂ воспользуемся краевыми условиями (1.27). В результате получим

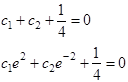
Откуда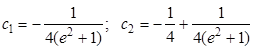

Следовательно, функция, дающая минимум функционалу (1.28) при условии (1.27), будет иметь вид

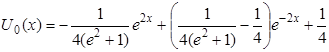.(1.30)

Пример 2.

В качестве второго примера рассмотрим задачу о брахистохроне.

Как было показано ранее (см. 1.2.1), задача состоит в том, чтобы найти функцию у = u(х), удовлетворяющую условиям:

u(0) = 0, u(а) = b

и сообщающую минимум функционалу

.

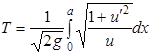В этом случае

.(1.31)

Функция (31) при u = 0 терпит разрыв. Путем несложных рассуждений показывается, что все-таки можно воспользоваться уравнением Эйлера в виде (1.26).

Уравнение (1.26) приводится к виду

(1.32)

Отсюда

.

Положим . Тогда .

Дифференцируя это выражение, получим . Замена дает дифференциальное уравнение относительно

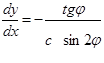
Далее

.

Положив , получим