Курсовая работа: Вариации при исчислении
(1.42)
За D(J) можно принять множество тех функций из С [a, b], которые обращаются в нуль при x=a и x=b (условие 3), а за 
– множество функций из С[1] [a, b], удовлетворяющих тем же условиям (1.3). Очевидно 
пересечение 
не пусто. Будем считать, что функционалы 
удовлетворяют требованиям 1,2,3. Пересечение линейных многообразий само есть линейное многообразие, поэтому существует элемент 
и линейное многообразие 
такое, что любой элемент 
имеет вид 
.
Будем считать, что множество 
плотно в рассматриваемом пространстве.
Справедлива теорема, принадлежащая Эйлеру и известная под названием правила множителей для изопериметрической задачи.
Теорема Эйлера: Пусть элемент 
решает изопериметрическую задачу. Если существуют такие элементы 
, что определитель
(1.43)
отличен от нуля, то найдутся такие постоянные 
, что
(1.44)
Рассмотренная теорема дает только необходимое условие минимума для изопериметрической задачи.
Техника решения изопериметрической задачи такова: составляя функционал
, (1.45)
где 
– неизвестные постоянные, и составляем для этого функционала уравнение Эйлера. Оно содержит в качестве неизвестных элемент u0 и постоянные 
. Эти неизвестные определяются из уравнения Эйлера (1.41) и изопериметрических равенств (1.41).
В качестве примера рассмотрим задачу о наибольшей площади (см. 2.2). В соответствии с теоремой Эйлера введем постоянный множитель 
и составим функционал
Уравнение Эйлера для функционала Э примет вид
Интегрирование дает
.
Отсюда
.
Интегрируя еще раз, придем к уравнению окружности радиуса 
. (1.46)
Таким образом, если решение существует, то это – дуга окружности. Для определения ее радиуса 
и центра 
имеем три уравнения
 |
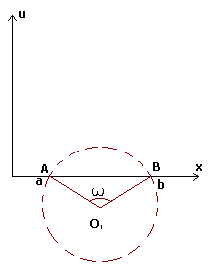| Рис. 1.2. |
.
Пусть 
будет угол, под которым виден отрезок AB из центра окружности (рис. 2):
.
Для определения имеем уравнение
,
решение которого всегда возможно при указанном выше условии. Подставляя условия (1.3) в уравнение (1.46) находим 
. Найдя 
из уравнения (1.46) найдем 
.