Курсовая работа: Вариации при исчислении

.

Последовательность элементов из D(J) называется минимизирующей для функционала J, если существует предел J(un), равный m.

Теорема 1: Функционал, ограниченный снизу, имеет по крайней мере одну минимизирующую последовательность.

Из определения нижней грани следует, что: 1) для любого элемента справедливо равенство ; 2) для любого существует такой элемент из D(J), что . Положим и обозначим 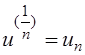. Тогда 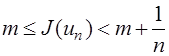, откуда следует, что .

Теорема 2: Пусть D(J) – линейное многообразие некоторого банахова пространства X. Если функционал J непрерывен в D(J) и существует предел минимизирующей последовательности , то элемент сообщает функционалу J минимальное значение.

Доказательство вытекает из непрерывности функционала

.

Теоремы 1, 2 создают возможность решать задачу о минимуме функционала, минуя уравнение Эйлера. Для этого надо прежде всего погрузить множество D(J) в такое банахово пространство X, в котором функционал J был бы непрерывен. Далее следует построить минимизирующую последовательность. Если она сходится, то ее предел решает вариационную задачу.

На этом построены численные вариационные методы (см 15) и обоснование их сходимости.

1.11 Функционал от функций, нескольких независимых переменных

Рассмотрим конечную область в m-мерном Евклидовом пространстве. Будем считать, что граница Г области состоит из конечного числа кусочно-гладких (m-1) – мерных поверхностей.

Рассмотрим функционал

(1.47)

при условии , где g(x) – заданная непрерывная функция на поверхности Г. Считаем, что выполнены требования 1, 2, 3.

Найдем первую вариацию функционала (1.47)

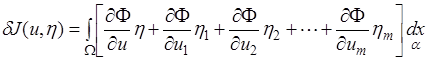(1.48)

Здесь обозначено

.

Пусть функция такова, что существуют обобщенные производные

.

Тогда имеем

и, следовательно

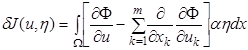(1.49)

В этом случае уравнение Эйлера для функционала (1.47) принимает вид

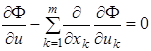, (1.50)

и называется уравнением Остроградского.

Пример.

Найти уравнение Эйлера для функционала