Курсовая работа: Вариации при исчислении

Таким образом, если решение задачи о брахистохроне имеет решение, то это решение есть циклоида.

1.8 Вторая вариация функционала. Достаточное условие минимума функционала

Рассмотрим функцию от вещественной переменной , считая и фиксированными.

Эту функцию разложим в ряд Тейлора:

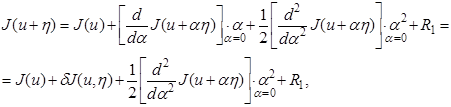(1.34)

где R1 – остаточный член ряда.

Выражение

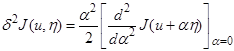
называется второй вариацией функционала J на элементе u.

Разложение (1.34) можно записать в виде

. (1.36)

Пусть функционал J достигает минимума, относительного или абсолютного на элементе u0. Тогда , и формула (1.36) дает

.(1.37)

Из этого соотношения вытекает достаточное условие того, что элемент u₀ , удовлетворяющий уравнению Эйлера (экстремаль), сообщает функционалу минимальное значение. Для абсолютного минимума это условие имеет вид (учитывая, что

(1.38)

для относительного минимума оно состоит в том, что неравенство (1.38) выполняется, когда элемент достаточно мал по норме.

Условие (1.38) в конкретных задачах трудно проверить, потому что величина обычно неизвестна, и непосредственно им, как правило, воспользоваться не удается.

Поэтому для проверки достаточного условия экстремума функционала пользуются более простыми условиями.

Запишем вторую вариацию для функционала (1.13)

пользуясь определением второй вариации (1.35)

,

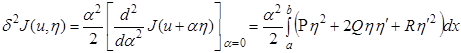где .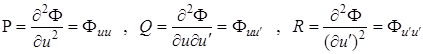

Так как , то, предполагая наличие соответствующих производных у Ф, интегрируя по частям и принимая во внимание, что , получим

, (1.39)

где .

Считаем, что необходимое условие экстремума выполнено, т.е. и для определенности будем говорить о минимуме функционала (1.13). Функция , как функция переменной при должна иметь минимум, следовательно, необходимым условием минимума является тот факт, чтобы при любом выборе . Можно показать, что отсюда непосредственно вытекает, что вдоль экстремали должно иметь место равенство .

Условие

называют условием Лежандра.